This article will deal with one interesting aspect of Number, that of Prime Numbers. Prime Numbers have often been thought of as being random. However one of the main tenants of the esoteric stream of knowledge is that the Universe is not random and chaotic. As we said earlier, chaos is a part of the Universe. It is not the Universe itself, or the process by which the Universe was created. Chaos can lead to order and systems that appear chaotic at certain levels are found to be ordered when viewing them from a greater perspective.
In this way we can see that order and intelligence exist in the universe and in nature. Prime numbers help us recognize this in a very ‘primal’ way.

“No branch of number theory is more saturated with mystery than the study of prime numbers: those exasperating, unruly integers that refuse to be divided evenly by any integers except themselves and 1.” Martin Gardner, 1964

Prime Numbers are only divisible by themselves and 1. There are 168 prime numbers between 1 and 1000. Here are the first 33:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137…
There are an infinite number of primes, as demonstrated by Euclid around 300 BC.
“Prime numbers are abundant at the beginning of the number line, but they grow much sparser among large numbers. Of the first 10 numbers, for example, 40 percent are prime – 2, 3, 5 and 7 – but among 10-digit numbers, only about 4 percent are prime. For over a century, mathematicians have understood how the primes taper off on average: Among large numbers, the expected gap between prime numbers is approximately 2.3 times the number of digits; so, for example, among 100-digit numbers, the expected gap between primes is about 230.”1
However, there are also ‘twin primes’ – pairs such as 3 and 5, or 11 and 13. Twin primes differ by only 2. It has long been speculated that there are infinitely many twin prime pairs. Yitang Zhang, in 2003, wrote a paper showing that “no matter how far you go into the deserts of the truly gargantuan prime numbers – no matter how sparse the primes become – you will keep finding prime pairs that differ by less than 70 million.”2
Prime Numbers have often been thought of as examples of the randomness of the universe.
Swiss mathematician Leonhard Euler (1707-1783) wrote, “Mathematicians have tried in vain to discover some order in the sequence of Primes and we have reason to believe that it is a mystery into which the mind will never penetrate.”

However, it has been found that there is structure to prime numbers. Methods such as Ulam’s Spiral and Sacks Spiral, as well as a radially arrangement of Prime Numbers along the axis of the cuboctahedron, and the Fibonacci Phyllotaxis Prime Number Sieve discovered by Dr. Scot C Nelson, are now shattering the conventional belief that prime numbers are random.
Mathematician Don Zagier, whose main area of work is number theory, wrote in 1975, “…despite their simple definition and role as the building blocks of the natural numbers, the prime numbers grow like weeds among the natural numbers, seeming to obey no other law than that of chance, and nobody can predict where the next one will sprout.”
He went on to say in 1977, “…there is no apparent reason why one number is prime and another not. To the contrary, upon looking at these numbers one has the feeling of being in the presence of one of the inexplicable secrets of creation.”

Prime Spirals
First Method: Ulam’s Spiral
The Ulam spiral was devised in 1963 by mathematician Stanislaw Ulam.
Ulam’s spiral is created by marking down numbers starting at 1 in a square spiral pattern, with 2 to next to 1 and 3 above 2, and so on as seen below.

Next circle all prime numbers or erase all non-primes as seen below.
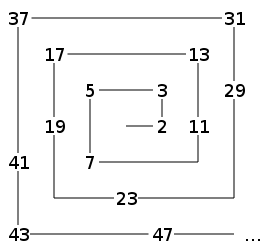
You will notice that the primes seem to be lining up on diagonal lines. When using 40,000 numbers the diagonal stripes can clearly be seen. However the stripes are broken up – they are not continuous.

It is important to note that compared to randomness of the same number of digits, randomness does not show diagonal stripes at all. See the image below. It is a random distribution of black dots.

The prime pattern formed is not random.
The lines with high prime density are called ‘Golden Lines’.
The image below shows Ulam’s Spiral up to 100,000 terms. It is very beautiful and very geometric.

Second Method: Sacks Spiral
Sacks spiral originates from software engineer Robert Sacks in 1994.
Sacks spiral is created by writing the square numbers in a horizontal line across the page:
1, 4, 9, 16, 25, 36, 49, 64…
These numbers are then connected with Archimedean spirals.
Next, the other numbers (remaining non-square numbers) are evenly spaced in order around each spiral.
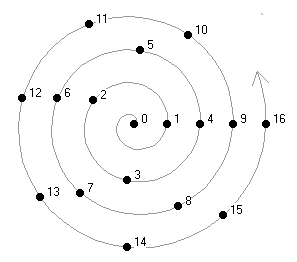
The primes form beautiful swooping and curving patterns.


The image below shows Sacks Spiral out to 100,000 terms. The long swooping curves are very beautiful.

Prime Numbers and the Cuboctahedron
“The cuboctahedron, or vector equilibrium, is the simplest geometric form that is in balance with the space it occupies, in perfect equilibrium on all sides.”3
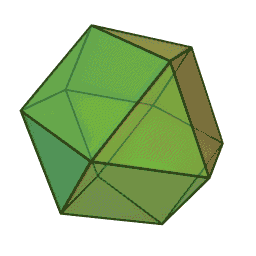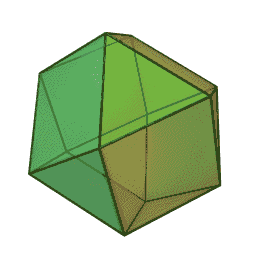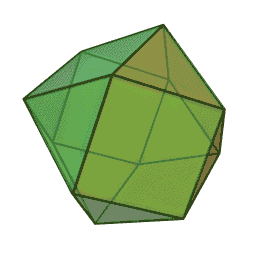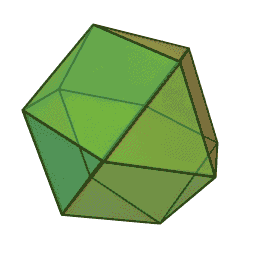
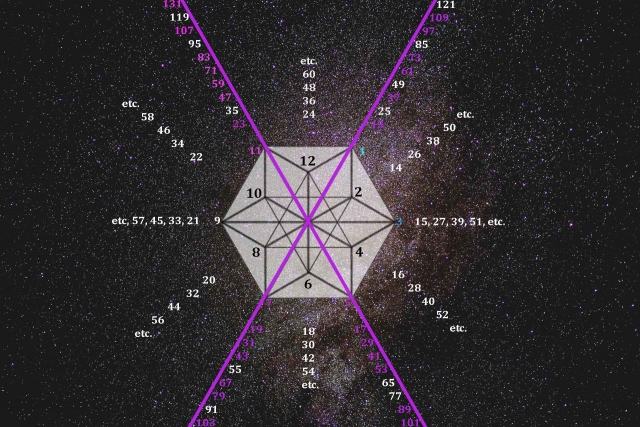
If the numbers are arranged in a radial pattern around its twelve points, starting at 1, all the prime numbers (except 2 & 3) line up along two of the six axes as seen below.
The primes above 3 are shown in purple.
We cannot verify if this pattern extends into infinity and can account for every single prime number, but it is an interesting pattern nonetheless.
We will examine the cuboctahedron in extreme detail over the course of this series. See Article 49.
Fibonacci Phyllotaxis Prime Number Sieve
The final prime pattern we will mention is from Dr. Scot C Nelson and his paper, “The Fibonacci Phyllotaxis Prime Sieve”.4
Wikipedia states “A prime number sieve is a fast type of algorithm for finding primes. There are many prime sieves. The simple sieve of Eratosthenes (250s BCE), the sieve of Sundaram (1934), the still faster but more complicated sieve of Atkin (2004), and various wheel sieves are most common.”
Prime number sieves involve arranging integers in various ways, starting with 2 and going up to any desired limit, then systematically marking out each number that is a multiple of 2, 3, 4, 5, 6, 7, 8, 8, 9…etc until nothing is left except primes.
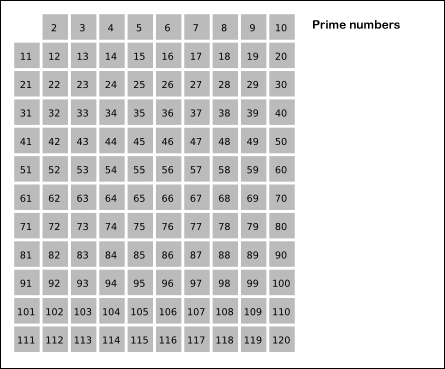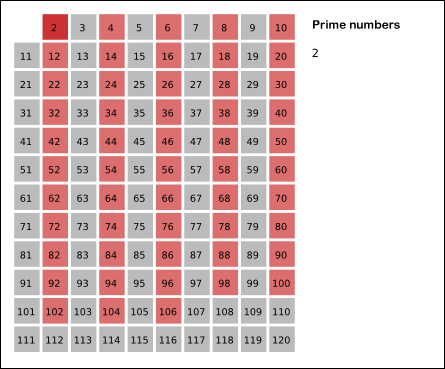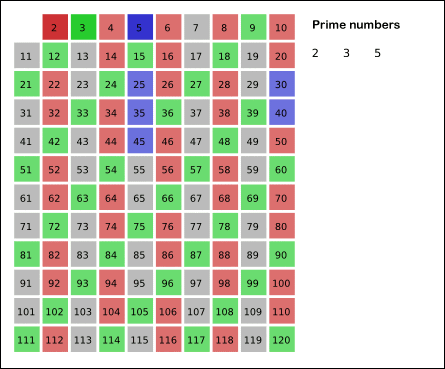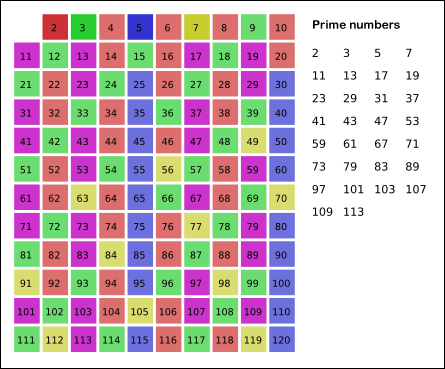
The animation below shows the sieve of Eratosthenes, up to 120, in action.
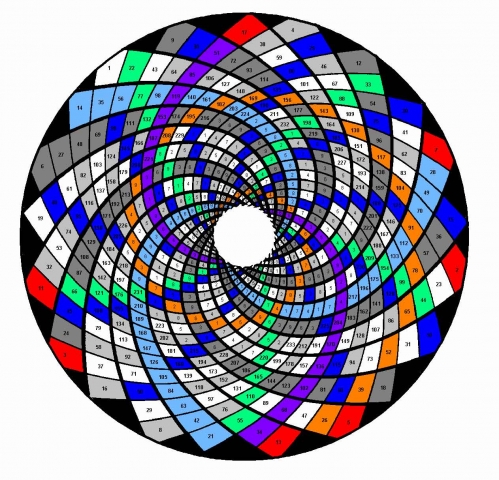
Dr. Nelson found that a daisy integer matrix has an unusual mathematical property: It serves as a simple and naturally efficient prime number sieve.
His conclusion: “The multiples of each prime number follow unique spiral paths along the surface of the flower from simple multiplication series associated with Fibonacci differences.”
His data reveals a mutual dependency between prime numbers and Fibonacci numbers, and the natural and central symmetry of prime numbers within three-dimensional objects.
The image below shows the daisy phyllotaxis prime sieve for the first 233 terms. Dr. Nelson concluded that the multiples of each prime number number follow unique spiral paths along the surface of the flower form simple multiplication series associated with Fibonacci differences.
The unshaded (white) pieces below are Prime Numbers.
Dr. Nelson goes on to explain:
Botanical objects literally contain a natural prime number generating algorithm within their structural growth algorithms. The multiples of each prime number emanate from primes along symmetrically unique spiral multiplication sequences in the matrix. This lends a natural beauty and elegance to the sieve and underscores the chief spatial importance of prime numbers within a biological matrix.
Multiples of primes are determined spatially by the relationship of a prime number to an evenly divisible Fibonacci number. Where primes are divisible by Fibonacci numbers, the natural symmetry of primes is expressed in the matrix of objects with Fibonacci phyllotaxis.
The middle image below represents Fibonacci phyllotaxis. This phyllotaxis patterns is represented by the Golden Angle which is approximately 137.5°.
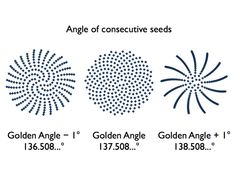
Phyllotaxis is the spatial and temporal arrangement of leaves or subunits around a stem or plant axis. The subunits emerge singly and in succession, retaining spatiotemporal relation to each other and to the central axis. Growing and expanding together, they harden into the shapes of common biological objects such as pine cones, pineapples, or flowers.
Articles 178-187 discuss phyllotaxis and the geometry of plants in great detail.

Chaos Theory: Order in Chaos
This discussion of order found among ‘randomness’ invariably leads us to a brief mention of Chaos Theory.
“Chaos is an interdisciplinary theory stating that within the apparent randomness of chaotic complex systems, there are underlying patterns, constant feedback loops, repetition, self-similarity, fractals, self-organization, and reliance on programming at the initial point known as sensitive dependence on initial conditions.”5

Chaos theory deals with deterministic systems whose behavior, in principle, can be predicted. Chaotic systems are predictable at first then ‘appear’ to become random.
Their behavior, nevertheless, is not random. It is just so complex it becomes practically impossible to predict.
“Throughout the universe, there are systems that, despite being inherently chaotic and unpredictable, tend to naturally become ordered.

Chaotic systems sound like systems destined for disorder and destruction, so where’s all this self-organizing, self-preserving order emerging from?”6
Could it be coming from the metaphysical reality of consciousness – the underlying foundation of physical reality that is geometric, harmonious and ordered?
We see that chaos is responsible for maintaining order in the natural world. 
“Feedback mechanisms not only introduce flexibility into living systems, sustaining delicate dynamical balances, they also promote nature’s propensity for self-organization. Even the beating heart relies on feedback for regularity.”7
This mention of the need for feedback leads us once again to the idea that there is a continual consciousness feedback loop that occurs between the physical and metaphysical realms as reality is constantly adjusted according to new input. Without this continual feedback, self-organization, growth and evolution could not occur. Results must be known in order to determine if they are working or if adjustments need to be made. This feedback (on many levels) is essential for all living systems.
“An important reflection we can learn from The Chaos Theory is the ever-changing flow of life. There’s an infinite amount of possibilities in between the plans and pursuits we dream up in our own realities. They are called OUR realities because we build them with our minds equipped with our own truths. The life we have been living is the life we have chosen for ourselves because it is what we believe we deserve. In the event that we find ourselves longing for another kind of life, we can weave it into the wonderful chaos that is our reality.”8

Conclusion
We have taken a look at various ways to arrange and view the prime numbers, discovering that there is an underlying pattern and design to the system. Even though we may not fully understand the pattern, it can be acknowledged that there is a pattern, and prime numbers are not random.
This backs up the important aspect of the esoteric stream of knowledge – that the universe is not chaotic and random, but is intelligently ordered, and, as Pythagoras and Plato taught, we can gain a deeper understanding of the universe through studying number.
As Anthony Morris writes, “Life is the result of an inherent numerical, geometric, musical and cosmological template that pervades the created Universe and has done so since the moment of its inception.”

- https://www.wired.com/2013/05/twin-primes/
- ibid.
- http://joedubs.com/prime-cubocohedron/
- www.rexresearch.com/rodin/9-nelsonfibophyllo.pdf
- https://en.wikipedia.org/wiki/Chaos_theory#cite_note-14
- Hill, Kyle, Nietzsche’s Butterfly: An Introduction to Chaos Theory, 4 September 2013, https://www.nature.com/scitable/blog/student-voices/nietzsches_butterfly_an_introduction_to
- Order into Chaos, New Scientist, 21 October 1989, https://www.newscientist.com/article/mg12416877-400-order-into-chaos/
- The Order in Chaos Theory, 12 November 2015, //medium.com/@universalintelligencespace/the-order-in-chaos-theory-192e2d67154a“>https://medium.com/@universalintelligencespace/the-order-in-chaos-theory-192e2d67154a>
Recent Comments