Return to Free Library

Return to Number Menu

Previous Article                                                                         Next Article

In this article we will take a closer look at some technical aspects of number that are essential to understand when it comes to the study of sacred geometry, harmony and the esoteric sciences.

Starting with a quote from Scott Olsen, he reminds us, “Nature holds a great mystery, zealously guarded by her custodians from those who would profane or abuse the wisdom. Periodically, portions of this tradition are quietly revealed to those of humanity who have attuned their eyes to see and ears to hear. The primary requirements are openness, sensitivity, enthusiasm, and an earnestness to understand the deeper meaning of nature’s marvels exhibited to us daily. Many of us tend to walk through life half asleep, at times numbed, if not actually deadened to the exquisite order that surrounds us.

But a trail of clues has been preserved.”

One such of these clues is the body of knowledge we’ve been discussing called the Quadrivium. This is the four-petaled area of study that includes: Number, Geometry, Music/Harmony, and Cosmology/Astronomy.

The Sacred Number Canon was introduced in Article 4. Now we will look at a more technical aspect of number, that regarding ratios and proportions.

Number as Relationships

John Michell writes in The Dimensions of Paradise, “A number on its own has no inherent meaning; its symbolism arises purely from its relationships to other numbers.”

Recall from Article 2 that Bucky Fuller said, “Geometry is the study of relationships.”

Ratios

The relation of one number to another is called a ratio. Ratios are a comparison of two different sizes, quantities, qualities or ideas.

Ratios are expressed a:b and they constitute a measure of difference, such as 4:8.

Robert Lawlor says of ratios, “Not only then is a ratio a:b the fundamental notion for all activities of perception, but it signals one of the most basic processes of intelligence in that it symbolizes a comparison between two things, and is thus the elementary basis for conceptual judgment.”

That is, ratios represent the compare/contrast function of our rational thinking.

As we will see, proportions involve the compare/contrast function on a new level, representing the correlating/synthesizing aspect of our intuition as we learn to harmonize seeming differences into greater wholes.

Logos as Ratio

It is interesting to note here that the word Logos means Ratio.

In Greek, logos means: word, saying, speech, discourse, thought, proportion, ratio, reckoning, gather, speak.

In philosophy, Logos refers to the rational principle that governs and develops the universe.

In Christianity, Logosrefers to ‘The Word’.

“In the beginning was the Logos (Word), and the Logos was with God, and the Logos was God.” John 1:1.

The Word = Sound = Pure Vibration. It represents the essential nature of all that exists.

At its core this means Vibration (wavelength, frequency, harmonics) is the Source of all Creation, and All Vibration flows geometrically. This is a cornerstone idea of the esoteric stream of knowledge on which all else is built.

The universe springs forth from the Word, which is Sound/Vibration/Frequency/Harmonics resulting from movements of consciousness. This fundamental idea has been preserved in many religious and spiritual traditions besides the Abrahamic religions (Christianity, Judaism, and Islam).

It is called Nada in India;

Nun in ancient Egypt;

the Music of the Spheres by Pythagoreans;

the Three Sacred Songs by the Aboriginal Australians

and the ever-present AUM of Hinduism and Buddhism.

These are only a few examples.

The Word, Divine Thought, or Cosmic Consciousness, gives rise to the fractioning of Unity. This fractioning of Unity is the act of Creation itself (the Many coming from the One). We will return to this topic again and again, analyzing this idea from both a scientific viewpoint and a spiritual viewpoint.

For now, try to understand that whenever we talk about ratios and proportions we are talking about a comparison between the vibration, frequency and harmonics of energy/light/sound.

Proportions

“Proportion is both an idea and a reality,” writes Keith Critchlow.  “It is the significant relationship between things, and therefore it is inherent in natural law, as we live in a cosmos – a cosmos being a profound unity of balance between various forces, events and elements.  Proportion in the broadest sense is concerned with this balance, harmony and relatedness between things: between body and mind, nature and humanity, illusion and reality…

The mark of a civilization is its concern for universal principles of order and the relationship of people to their universe…Humanity’s relation to things is the key, and the motivation towards both logos and proportion arises from the need to be in the right relationship with the inner and the apparent outer essence of the cosmos…

The role of proportion is to aid us in understanding the mysterious way in which Unity unfolds into multiplicity so that we can use this knowledge to reintegrate ourselves by the same mystery…

It must be our wholeness that is being aware of the parts of our experience – and possibly the most simple definition of sanity is wholeness of mind.”

A proportion is a repeating ratio that typically involves four terms, such as 4:8 :: 5:10. This is called a ‘four-termed discontinuous proportion’. It is a relationship of equivalency between two ratios expressed as a:b :: c:d. For instance, in our example, we see that 4 is to 8 as 5 is to 10. The two sets of numbers are equivalent. 4 is half of 8 and 5 is half of 10.

“When we think with four elements, that is with two different ratios, we locate our thought within the range of manifestation of the natural world since four is the number-symbol indicative of the finite, rational, measurable world of procreated form.” Robert Lawlor

In proportions, there are no fixed quantities, only fixed relationships.

As we said above, proportions represent differences coming together to form greater wholes.

Returning again to Lawlor, he states, “[A proportion] represents a level of intelligence more subtle and profound than the direct response to a simple difference which is the ratio, and it was known in Greek thought as analogy.”

“In all realms of our experience,” says Gyorgy Doczi, “we are finding the need to rediscover proper proportions.  The proportions of nature, arts, and architecture can help us in their effort, for these proportions are shared limitations that create harmonious relationships out of differences.  Thus they teach us that limitations are not just restrictive, but they also are creative.”

There are three important proportions we will discuss here:

• Arithmetic Proportion
• Geometric Proportion
• Harmonic Proportion

These proportions are inextricably related to the concept of harmony, specifically musical harmony and harmonious musical intervals. We will discuss this in more detail in Articles 69-70.

We will first discuss mediation.

Mediation

Mediation is the binding of two extremes by a single mean term, or

the binding of two “opposite” tones by harmoniously placing a third tone between them.

We respond not to the tones themselves, but to their relationship – their musical interval.

Mediation and Proportion

A mediating proportion can be defined as “A group of three unequal numbers such that two of their differences are to each other in the same relationship as one of these numbers is to itself or to one of the other two numbers”.

We will now break this statement down to better understand what it means.

A median proportion is formed from a group of any three numbers with a greater than b and b greater than c (a > b > c), such that “two of their differences”:

a – b (this is one difference)

b – c (this is the second difference)

“…are to each other” :

a – b : b – c

“…in the same way as one of these numbers is to itself”

(Case 1) a – b : b – c : : a : a or

a – b : b – c : : b : b or

a – b : b – c : : c : c

‘…or as one of these numbers is to one of the other numbers’:

(Case 2) a – b : b – c : : a : b or

(Case 3) a – b : b – c : : a : c.

Three Major Medians

Arithmetic Proportion (Case 1)

Arithmetic: b = (a + c)/2

3, 5, 7 is an arithmetic progression with arithmetic mean, b = 5.

5 = (3 + 7)/2

This contains the law for addition and its inverse subtraction.

It describes the relationship which gives the natural series of cardinal numbers, 1, 2, 3, 4, 5, 6…etc.

Each term is obtained by adding a fixed number to the previous term. They increase by the same number each time. The image below shows an arithmetic progression obtained by adding 2 to each new number.

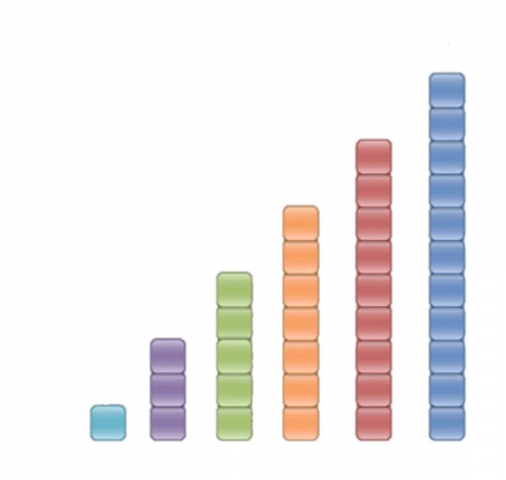
It shows an equality of difference, but inequality of ratio.  This means when each term is subtracted from the term in front of it you will always get the same number. However when the terms are divided you will not get the same number.

For instance: 3 – 1 = 5 – 3 = 7 – 5…etc. This is the equality of difference.

But 11/9 does not equal 9/7 or 7/5 or 5/3. This is the inequality of ratio.

“In the arithmetic progression, then, addition is the means of growth, whereas in the progression called “Geometric” (an example of which is 2, 4, 8, 16…) each successive term unfolds by being multiplied by the first term.  Thus,” Robert Lawlor tells us, “addition and multiplication remain our two most effective mathematical metaphors for describing organic growth on the one hand and physical or gnomonic accumulation on the other.”

Geometric Proportion (Case 2)

Geometric: b² = ac

4, 8, 16 is a geometrical progression with geometric mean, b = 8.

8² = 64 = 4 x 16

This contains the law for multiplication and its inversion, division.

It describes the relationship which gives any series of geometric progression.

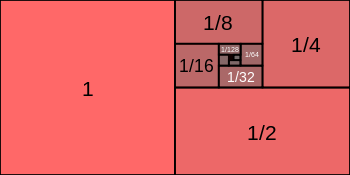
It shows equality of ratio but inequality of difference.

For instance, in the progression 2, 4, 8, 16, 32:

4 – 2 does not equal 8 – 4 or 16 – 8. This is the inequality of difference.

But 32/16 = 16/8 = 8/4 = 4/2. This is the equality of ratio.

It is called the ‘perfect proportion’ because it is a direct proportional relationship, an equality of proportion bound by one mean term.

Robert Lawlor writes, “Nicomachus and other Greek philosophers considered it as the only one which can be regarded as strictly analogos. It is the perceiver himself (b) who forms the equivalency or identity between observed differences (a and c). The perceiver no longer stands outside the comparative activity as in the four-term, discontinuous or disjunctive mode, which images the perceived difference as being separate ratios or distinctions.”

Harmonic Proportion (Case 3)

Harmonic: b = (2ac)/a+c

2, 3, 6 is a harmonic progression with harmonic mean, b = 3.

3 = 24/8 = (2 x 2 x 6)/2+6

This proportion is derived from a combination of both the additive and multiplicative growth procedures of the other two progressions.

It is formed by a multiplication of any two extremes (a, c) followed by the division of this product by their average or arithmetic mean (a + c)/2.

Another example: given two extremes (a, c) = 6 and 12

The products of 6 and 12 = 72

The arithmetic mean between 6 and 12 = 9

72/9 = 8

So: 6, 8, 12 is a harmonic progression.

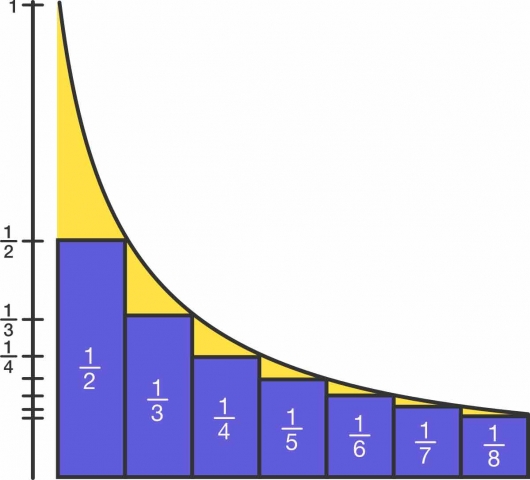
The most important and mysterious characteristic of the this type of progression is the fact that the inverse of every harmonic progression is an arithmetic progression.  Thus 2, 3, 4, 5…is an ascending arithmetic progression, while the inverse series (1/2, 1/3, ¼, 1/5…) is a descending harmonic progression.

Example: 2, 3, 4, 5 = ascending arithmetic progression

½, 1/3, ¼, 1/5 = descending harmonic progression

“These two parallel yet inversing progressions not only provide the foundations of music, but more generally provide a mathematical model with which to investigate the complementary or opposed symmetries of a dualized, yet harmonically integrated, whole.  For this reason the musical metaphor was the cornerstone of ancient philosophy, applicable to both physical and metaphysical domains.” ~ Robert Lawlor, Homage to Pythagoras

For now, the important thing is to remember the importance of Number as relationship, rather than mere quantities.

Supra-rational Numbers (Irrational Numbers)

“The curious fact,” writes Keith Critchlow, “is that as we get further into the mathematical aspect of proportion we begin to find those exceptionally subtle ratios known as the transcendentals, which have the rare quality of being indescribable in whole numbers, while remaining precise relationships geometrically.”

Critchlow continues: “Whole numbers belong to one order of mathematics and because they have a precise quantity, are associated traditionally with the earthly order. Transcendentals or incommensurables are related to proportional ratios, regular polygons and pi. They can be taken to be of the same symbolic order as that of squaring the circle – rationalizing the irrational – unifying the paradox.”

A rational number is a real number than can be written as a ratio. That means it can be written as a fraction in which both the numerator and denominator are whole numbers. It is also a simple whole number. These are the numbers we are most familiar with.

An irrational number cannot be expressed as a ratio. It cannot be written as a simple fraction because there is not a finite number of digits when written as a decimal. Instead, the numbers in the decimal go on forever, to infinity, without repeating.

“Irrational numbers are not unreasonable; they are only beyond reason, in the sense that they are beyond the grasp of whole numbers.  They are infinite and intangible.  In patterns of organic growth the irrational phi ratio of the golden section reveals that there is indeed an infinite and intangible side to our world.” ~ Gyorgy Doczi

In sacred geometry and esoteric science, we refer to these as supra-rational numbers or transcendental numbers.  They are a key opening a door to a higher reality of Number.

Robert Lawlor teaches us that within the concept of Number lie two aspects:

The exoteric – the external, definite, finite, particularizing power (compare/contrast function of consciousness). This refers to the uniqueness and distinctions among different things.

The esoteric – the inner, universal synthesizing power (correlate/synthesize function of consciousness). This refers to the unity and interconnection amongh different things.

These are key ideas that reflect the very nature of reality itself and the two natures of existence: the seen, material, physical reality (and that of identifying individuality within creation) and the unseen, spiritual, metaphysical reality (that of identifying unity within all creation).

Rational numbers are examples of the exoteric aspect and Supra-rational numbers are examples of the esoteric aspect.

Examples of Supra-rational Numbers

Pi

• π = 3.14159265359…
• Pi is the ratio of a circle’s circumference to its diameter.
• See Article 12 for more information.

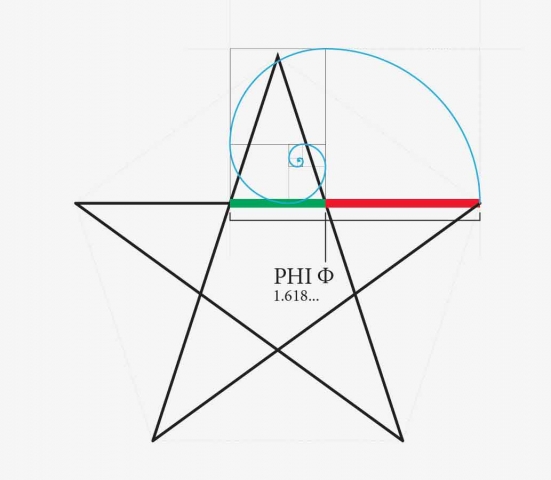
The Golden Ratio

• φ = 0.61803398875… (pronounced ‘fee’)
• Φ = 1.61803398875… (pronounced ‘fi’)
• The golden ratio is the ratio that divides any line, plane or volume in such a way that the shorter portion is to the longer portion as the longer portion is the whole.
• Symbolically the golden ratio shows us how we can be a ‘portion of the whole’ and ‘the whole’ simultaneously; or how we can be both finite and infinite simultaneously.
• See Articles 56-60 for more information.

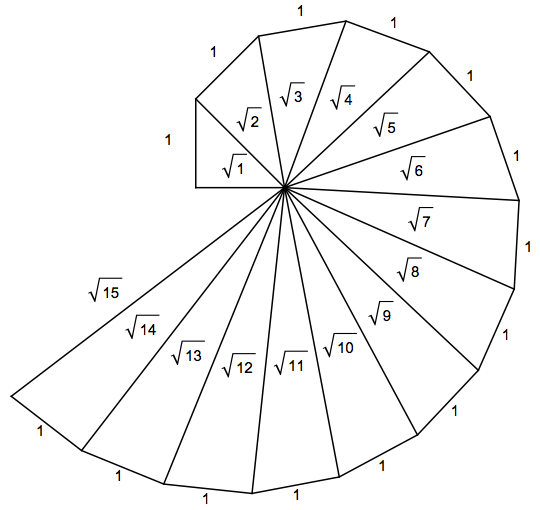
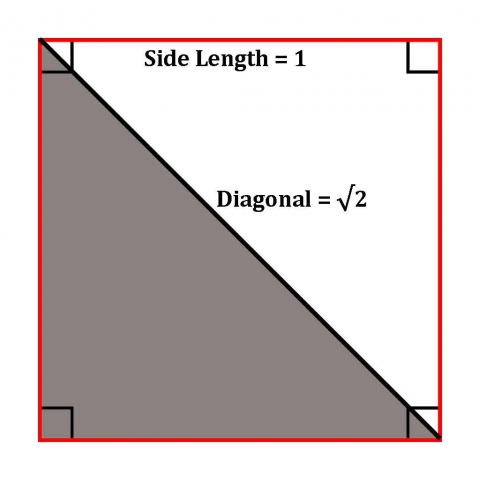
Square Roots

• √2 = 1.41421356237…
  • The ratio of the diagonal of the square to the side length of the square.

• √3 = 1.732050807569…
  • The ratio of the height of an equilateral triangle to half its base length.

• √5 = 2.2360679775…
  • The ratio of the diagonal of the double square to the length of its long side.
  • Phi = (1 + √5)2

• See Articles 24-26 and 37 for more information.

Exponential Growth Function (e)

• e is the base of the natural logarithm.
• It is the sum of the infinite series.
• e = 2.71828182846…
• e = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

2! 3! 4! 5! 6! 7!…

• [!] represents a factorial – for example: 4! = 1 x 2 x 3 x 4

An interesting side note – The sun’s circumference is e million miles:

Concerning all supra-rational numbers, these numbers can be rounded off and treated like any other number, but they can never be reduced to a quantity. They are relationships.

Supra-rational Numbers as Numerical Functions

We are starting to see how Number can be considered as a formal relationship. This type of numerical relationship is called a function.

For example, take a circle with value 1 for the diameter and take a square with value 1 for the side length.

In the first case, the circumference of the circle will be incommensurable – that is, an irrational number. The circumference would be π or 3.14159…

π is the functional number of a circle.

In the second case the diagonal of the square will be incommensurable. The diagonal would be √2 or 1.4142…

√2 is the functional number of a square.

This principle remains the same in inversion. If the circumference of the circle and diagonal of the square are set at 1, the circle’s diameter and the square’s side length will be incommensurable.

In geometry, the formal relationship of (diagonal : side) or (circumference : diameter) are knowable self-evident realities: 1 : √2 and 1 : π.

Robert Lawlor states, “No matter what quantities are applied to the side and to the diameter the relationship will remain invariable, for in essence this functional aspect of Number is neither large nor small, neither infinite nor finite: it is universal.”

These Supra-rational functions of numbers demonstrate that Number is above all a relationship.

Conclusion

This article introduces the key concept of ratios, proportions, and supra-rational numbers. We will return to these concepts again and again. For now, it is important to recognize these numbers when you come across them. Pi (π), Phi (Φ), and the square roots (√) of 2, 3, and 5 will come up over and over again and are extremely important aspects of understanding sacred geometry and the esoteric sciences.

To end this article let us return once more to John Michell and The Dimensions of Paradise. He writes, “In their cosmological inquires, the ancients paid less attention to physical phenomena than to the study of number. In the fixed ratios of arithmetic, they discerned a constant reality (‘that which always is and never becomes’) as distinct from the apparent but illusory world of phenomena (‘that which is always becoming but never is’).”