“Prior to the current tyranny of the materialistic, mechanical model of our universe, the wise people of all traditional cultures viewed the world as a continuous spectrum.” Keith Critchlow

Pythagorean Mathematics
Manly P Hall writes in The Secret Teachings of All Ages, “The Pythagoreans declared arithmetic to be the mother of the mathematical sciences. This is proved by the fact that geometry, music, and astronomy are dependent upon it but it is not dependent upon them. The Pythagoreans also demonstrated arithmetic to be prior to astronomy, for the latter is dependent upon both geometry and music. The size, form, and motion of the celestial bodies is determined by the use of geometry; their harmony and rhythm by the use of music.”
In this article we will once again delve into the foundational science of the Quadrivium – that of Number. We will specifically take a look at number and arithmetic as it was taught by Pythagoras over 2500 years ago. Remember, the attributes of numbers belong inherently to musical scales, to the orbits of the planets, to cosmic time cycles and to many other things. Thus number is the root of a harmonic-geometric waveform Universe.
Pythagoras defined number to be the extension and energy of the generative reasons contained in the Monad. The God of Pythagoras was the Monad, the ‘One that is Everything’ and was represented by a circle. Just as all polygons come from a circle and all polyhedra come from a sphere, everything in reality comes from the Monad, “the Supreme Mind distributed throughout all parts of the Universe – the Cause of all things, the Intelligence of all things, and the Power within all things.”

Multitude & Magnitude
Number is a term applied to all numerals and their combinations. There are two parts to the Science of Mathematics: Multitude and Magnitude.
Multitude refers to the constituent parts of a thing.

There are two parts to multitude: That is the way a thing relates to itself, and the way a thing relates to other things. In the Pythagorean viewpoint, the relation to itself has priority over the relation to others.
What this means is that it is far more important to know and understand your own self – your own mind, motivations, expectations, beliefs, emotions and thoughts, than to try to understand another’s.
“First know thyself.” Then you will know others.

The knowledge of the mind is the knowledge of creation.
Magnitude refers to the relative size or density of a thing.
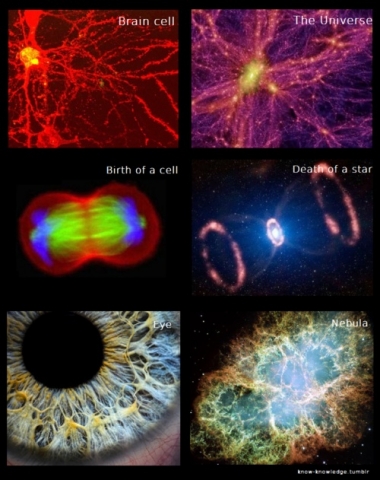
There are two parts to magnitude: Magnitude which is stationary, and magnitude which is movable. In the Pythagorean viewpoint, magnitude which is stationary has priority over magnitude which is movable.
This means there are two aspects of ourselves and the universe. The first is the metaphysical ‘Source’ aspect – that which is stationary, stable, ever-true, eternal – the Spirit. The second is the physical material aspect – that which is movable, changeable, cyclic – the Body.
The stationary, being the Source, or that which came first, will always have priority over the movable, the transient materialistic aspects of reality, whether they be our bodies themselves or the temporary aspects of life: material goods, wealth, jobs, changing relationships, seasons, age…etc.
Manly P Hall tells us, “Both multitude and magnitude were circumscribed by the circumference of mind.” What this means is that we are not strictly talking about numerals when we speak of ‘a thing’. On one level we are talking about the mind itself – the consciousness and perspectives of each human being. On another level, we are talking about the universe itself – the Cosmic Consciousness and how the parts of the universe relate to other parts.
It will be stressed again and again: Any study of number has far less to do with quantities and calculations, and far more to do with recognizing the symbolism behind numbers and how they represent the different aspects of consciousness, of spiritual evolution, and of the creation and evolution of the Universe through sound, vibration and waves.
Odd & Even
There are two orders of Number: Odd & Even. John Michell writes, “The division of numbers into the odd and the even reflected the division of the universe into positively and negatively charged elements.”1
Here we are not only talking about the positive and negative charges in electricity, or the positive and negative poles of a magnet, but we are talking about the polarity of consciousness – the positive and negative aspects of our thoughts, beliefs and feelings.

Positive aspects bring us closer to unity and they involve harmony and order. Negative aspects take us farther away from unity – heightening our separation, and they involve chaos and disorder. Obviously these positive and negative aspects can exist within an infinite spectrum of magnitude and multitude and they are both integral parts of reality.
This primal separation from Unity – the Monad – is called the Dyad, and is represented by the number 2.
The Pythagoreans considered the odd numbers to be definite and masculine. They considered the even numbers – of which the Dyad was the prototype – to be indefinite and feminine.
Odd Numbers
The odd number cannot be divided equally because unity or 1, always remains indivisible.
For instance:
9 = 4 + 1 + 4
19 = 9 + 1 + 9
153 = 76 + 1 + 76…etc.
It is helpful to begin to see odd numbers in this way. Each odd number revolves around the central axis of unity. Although the number is separated or fractured, it retains its connection to unity. In fact, its parts continually whirl around unity like water whirls around a drain, or like a dog chases its tail, circling round and round, and in the case of numbers, never stopping. This gives it a quality of movement and action – hence represented by the active masculine principle.
Furthermore, if any odd number be divided into two parts, one part will always be odd and the other even.
For instance:
9 = 4 + 5
19 = 9 + 10
153 = 76 + 77…etc.
Manly P Hall tells us that Unity, or 1, was considered an androgynous number, partaking of both the masculine and the feminine attributes; consequently both odd and even. For this reason the Pythagoreans called it evenly-odd.
Even Numbers
The even number can be divided into two equal parts, which are always either both odd or both even.
For example:
10 = 5 + 5
144 = 72 + 72
360 = 180 + 180
You can see how the even numbers contain the quality of passivity. They are equal and static. They do not contain the inherent motion of the odd numbers that continually whirl around attempting to balance their parts. Hence the even numbers represent the passive feminine principle.

Classes of Odd Numbers
There are three general classes of odd numbers: incomposite, composite and incomposite-composite.
Incomposite numbers are Prime Numbers. They have no divisor other than themselves and unity.
Examples are: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41…etc.
Read Article 9 for more information about prime numbers.
Composite numbers are divisible not only by themselves and unity but also by some other number.
Examples are: 9, 15, 21, 25, 27, 33, 39, 45, 51, 57…etc
15 is divisible by 15 and 1 but also by 3 and 5.
39 is divisible by 39 and 1 but also by 3 and 13.
57 is divisible by 57 and 1 but also by 3 and 19.
Incomposite-Composite numbers have no common divisor, although each of itself is capable of division, such as 9 and 25.
This means they are divisible by themselves and unity, and also 1 single other number.
Because they have individual divisors they are called composite.
Because they have no common divisor (such as the common 3 above) they are called incomposite.
Classes of Even Numbers
There are three general classes of even numbers: evenly-even, evenly-odd, and oddly-even.
Evenly-even numbers are all in duple ratio from unity. These numbers can be halved and the halves again halved back to unity.
For example:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024…etc.
Ex. 128/2 = 64; 64/2 = 32; 32/2 = 16; 16/2 = 8; 8/2 = 4; 4/2 = 2; 2/2 = 1
Evenly-even numbers possess certain unique properties. The sum of any number of terms but the last term is always equal to the last term minus one.
For example:
The sum of the first 2 terms (1 + 2 = 3) equals the third term (4) minus 1 (3), or:
The sum of the 1st, 2nd, 3rd and 4th terms (1 + 2 + 4 + 8 = 15) equals the 5th term (16) minus 1 (15).
The sum of terms 1 to 10 = 1023. This equals the 11th term (1024) minus 1 = 1023.
This applies for all terms in this series.
This evenly-even series represents the process of doubling seen in cell division and the structure of octaves.
Remember, numbers aren’t static ‘things’. They represent processes.
Evenly-odd numbers are numbers which, when halved, are incapable of further halving. They are formed by taking the odd numbers in sequential order and multiplying them by 2.
Odd numbers 1, 3, 5, 7, 9, 11 produce the evenly-odd numbers 2, 6, 10, 14, 18, 22.
Starting with 2, every fourth number is evenly-odd.
The number to be divided is the dividend. The number which divides is the divisor. The result of the division is the quotient.
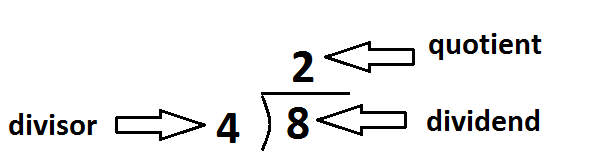
For example: In 360/6 = 60, 360 is the dividend. 6 is the divisor. 60 is the quotient.
If the divisor be odd the quotient is always even. For example:
18/3 (odd divisor) = 6 (even quotient)
If the divisor be even the quotient is always odd. For example:
18/2 (even divisor) = 9 (odd quotient)
Also, each term in the series is one-half the sum of the terms on either side of it. For example:
10 is half the sum of the terms on either side of it (14 + 6 = 20).
18 is half the sum of the terms on either side of it (22 + 14 = 36)…etc.
Oddly-odd or unevenly-even numbers are a compromise between the evenly-even and the evenly-odd numbers. Unlike the evenly-even, they cannot be halved back to unity; and unlike the evenly-odd, they are capable of more than one division by halving.
For example: 24 24 /2 = 12 12/2 = 6 6/2 = 3
Three Further Classes of Even Numbers
There are three other classes of even numbers: superperfect, deficient, and perfect.
Superperfect numbers have the sum of their fractional parts greater than themselves. For example:
The number 24:
½ of 24 = 12; ¼ of 24 = 6; 1/3 of 24 = 8; 1/6 of 24 = 4; 1/12 of 24 = 2; 1/24 = 1
The sum of these parts (12 + 6 + 8 + 4 + 2 + 1) = 33; which is greater than 24.
Deficient numbers are numbers that have the sum of their fractional parts less than themselves. For example:
The number 14:
½ of 14 = 7; 1/7 of 14 = 2; 1/14 = 1
The sum of the parts (7 + 2 + 1) = 10, which is less than 14.
Perfect numbers are those numbers that have the sum of their fractional parts equal to themselves. For example:
The number 28:
½ of 28 = 14; ¼ of 28 = 7; 1/7 of 28 = 4; 1/14 of 28 = 2; 1/28 = 1
The sum of the parts (14 + 7 + 4 + 2 + 1) = 28, which is equal to 28.
The perfect numbers are extremely rare.
There is only one between 1 and 10 = 6
One between 10 and 100 = 28
One between 100 and 1000 = 496
One between 1000 and 10000 = 8128
The 5th perfect number = 33550336
“Perfect numbers are beautiful images of the virtues which are certain media between excess and defect. On the contrary, an infinite multitude of superabundant and diminished numbers may be found, nor are they disposed in any orderly series or generated from any certain end; and hence they have a great similitude to the vices, which are numerous, inordinate, and indefinite.” Thomas Taylor, Theoretic Arithmetic
Number theory of Pythagorean mathematics may be some of the driest information included in the Cosmic Core thesis project, yet it is included because it is necessary to understand just what a profound importance number had in the ancient and esoteric philosophy and how numbers were seen not as quantities, but as symbols containing various qualities. These qualities of number were likened to the qualities of our thoughts, emotions and actions.
For any given thought, emotion, or action, you can contemplate its qualities. Does it contain harmony? Does it bring you peace? Does it anger you? Does it make you feel superior? Inferior? Does it make you want to harm something or yourself? Does it make you want to help? Does it make you feel powerful? Powerless? Fearful? Confident? Jealous? Compassionate? Confused? Uplifted?
The act of questioning your beliefs, your thoughts, emotions and actions as they occur is the single most important lesson to glean from this information. What thoughts bring us back towards unity and what thoughts separate us from others, or from ourselves? How close are these thoughts to unity and how far away? Numbers are symbols of these attributes of our consciousness – our very thoughts, emotions, beliefs, expectations and actions.
The perfect numbers are seen as those divine virtues – those pure, selfless thoughts and intentions that bring us straight back to unity – thoughts, emotions and actions that contain a perfect balance of wisdom and compassion, action and passivity, and strength and gentleness.

Gnomons
“Pythagoras taught that the experience of life in a finite, limited body was specifically for the purpose of discovering and manifesting supernatural existence within the finite. One’s concentration, then, should also be on the finite itself, to discover how this finite could contain intrinsically a power to express the infinite. This does not mean concentration on finite, material effects, but on the abstract principles revealed in the finite world, and the Causes which create and support this embodiment. Hence Pythagorean mathematics were limited to whole numbers, that is definable, arrested states, and sought after universal expressions with the measurable, geometric frame of the square, a profound symbol of finite perfection.” – Robert Lawlor, Sacred Geometry: Philosophy & Practice

Gnomonic growth is any figure, which, when added to another figure, leaves the resultant figure similar to the original.
This is tied in to Scale Invariance, or Fractal Self-similarity, which was discussed in Article 2 and will be discussed in much greater detail in future articles.
“Some things suffer no change other than magnitude when they grow”: This is the principle of gnomonic growth or scale invariance.

There can be gnomonic spirals, such as the golden spiral; shapes, such as proportional square root rectangles; numbers; architecture; and living systems, such as the Fibonacci sequence found extensively in nature.
The golden spiral is pictured below:

We will briefly discuss gnomonic numbers pertaining to Pythagorean mathematics, recalling to mind that ancient philosophers such as Pythagoras, Plato and Euclid did not have numerals to work with, but used small pebbles when studying numbers. Using this method, it is far easier to see the geometric nature of numbers.
Triangular Numbers
Triangular numbers increase in a triangular fashion, such as 1, 3, 6, 10, 15, 21…etc.
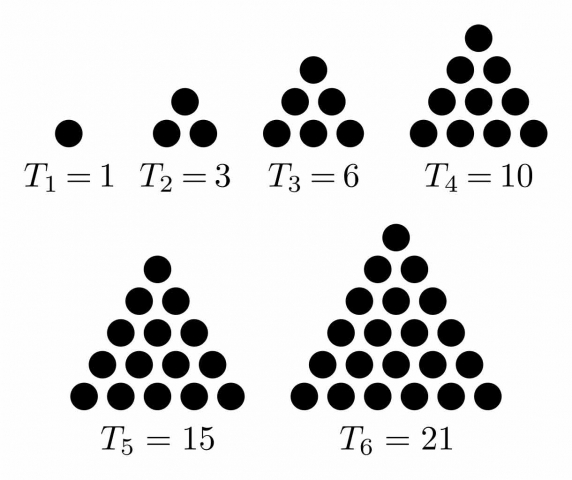
A triangular number consists of all the numbers from unity up to a given limit.
The series they form is:
3 (= 1 + 2)
6 (= 1 + 2 + 3)
10 (=1 + 2 + 3 + 4)
15 (=1 + 2 + 3 + 4 + 5)
21 (=1 + 2 + 3 + 4 + 5 + 6) and so on.
When arranged using pebbles, they form triangles.
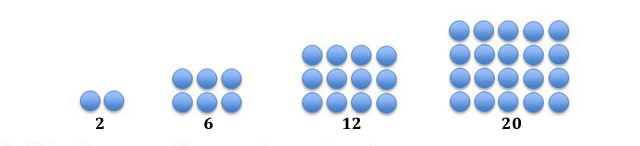
Rectangular Numbers
Rectangular numbers increase in a musical fashion based on octaves, such as 2, 6, 12, 20. When arranged using pebbles, they form rectangles.
Square Numbers
Square numbers are made up of two successive triangular numbers, such as 1, 4, 9, 16.

For example:
4 = 1 + 3
9 = 6 + 3
16 = 10 + 6…etc.
These numbers are the literal ‘squares’ of numbers:
22 = 4
32 = 9
42 = 16
52 = 25…etc.
When arranged using pebbles, they form squares.
Cubic Numbers
Cubic numbers are the literal ‘cubes’ of numbers, such as 1, 8, 27, 64, 125…etc.
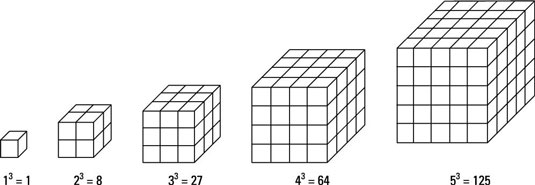
For example:
23 = 8
33 = 27
43 = 64
53 = 125
When arranged using pebbles in three-dimensions, they form cubes.
The Lambda
The Lambda is a numerical-geometric figure that was studied by the ancient Greeks. It was described by Plato in the Timaeus as the ‘World Soul’.

Plato states that God created the Cosmic Soul using two mathematical strips of 1, 2, 4, 8 and 1, 3, 9, 27.
These two strips follow the shape of an inverted “V” or the “Platonic Lambda”. Lambda is the 11th letter of the Greek alphabet. It is triangular in nature, like the tetraktys discussed below. The triangular form represents its divine nature.
“Plato holds continuous geometric proportion to be the most profound cosmic bond. In his Timaeus the world soul binds together into one harmonic resonance the intelligible world of forms (including pure mathematics) above, and the visible world of material object below, through the 1, 2, 4, 8 and 1, 3, 9, 27 series.”2
The result of Plato’s World Soul is the Lambda – an extended continuous geometric proportion.
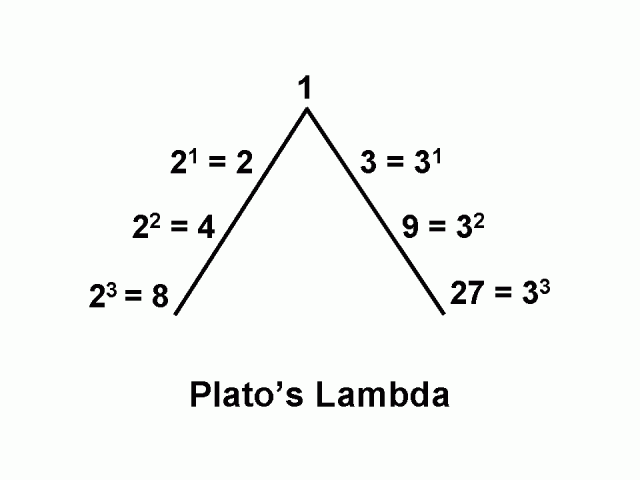
The First Series: 1, 2, 4, 8 is the doubling sequence. As we discussed above, the even numbers are associated with the passive feminine principle.
The Second Series: 1, 3, 9, 27 is the tripling sequence. These odd numbers are associated with the active masculine principle.
These two series together produce the full range of musical ratios – that is the octave (2:1), the fifth (3:2), the fourth (4:3) and the whole tone (9:8). We will discuss this in great detail in later articles.
Robert Lawlor explains: “In the arithmetic progression addition is the means of growth, whereas in the progression called “Geometric” (an example of which is 2, 4, 8, 16…) each successive term unfolds by being multiplied by the first term. Thus addition and multiplication remain our two most effective mathematical metaphors for describing organic growth on the one hand and physical or gnomonic accumulation on the other.
The type of progression, which combines both the additive and multiplicative growth procedures of the other two progressions, is called ‘harmonic’. The most important and mysterious characteristic of this form of harmonic, proportional progression is the fact that the inverse of any harmonic progression is an arithmetic progression. Thus 2, 3, 4, 5…is an ascending arithmetic progression, while the inverse series (1/2, 1/3, ¼, 1/5…) is a descending harmonic progression.
These two parallel yet inversing progressions not only provide the foundations of music, but more generally provide a mathematical model with which to investigate the complementary or opposed symmetries of dualized, yet harmonically integrated, whole. For this reason the musical metaphor was the cornerstone of ancient philosophy, applicable to both physical and metaphysical domains.”
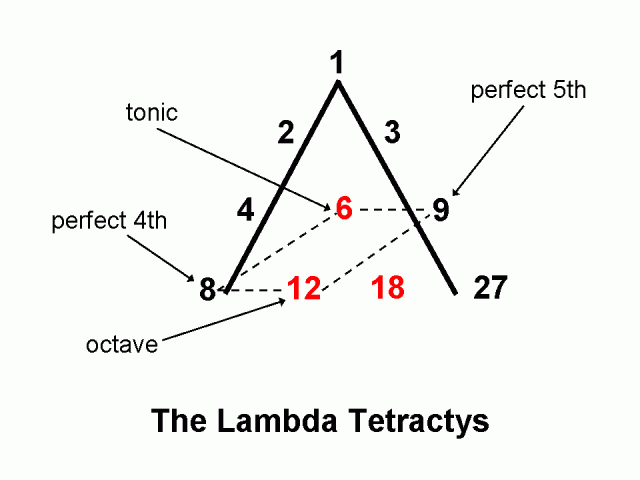
Robert Lawlor tells us, “Pythagoras is credited with first establishing the relationship between number ratios and sound frequencies. The whole number ratios for determining the consonant sounds in a musical scale are either drawn from or are multiples of the numbers in the two progressions of the Lambda.”
“Plato’s evident intention,” states John Michell about the Lambda, “was to identify number as the archetype of creation and to draw attention to those particular numbers that constitute its core and that, in various combinations, generate the entire field of number.”

The Tetraktys
The Tetraktys is another numerical-geometric figure that is associated with the Pythagorean school. We have mentioned this in previous articles.
Freddy Silva writes, “Although attributed to Pythagoras, the tetractys can be traced to the Hindus, and prior to them is a matter of conjecture. Like the Flower of Life, what is certain is the association of this figure with the creative process.
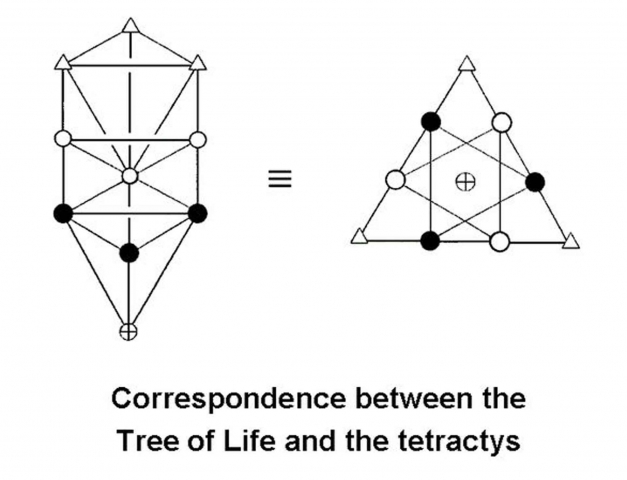
Theon of Smyrna, a renowned scholar in antiquity, declared that the ten dots of the tetractys represented the Ten Words of God. To Christians these ‘words’ signified the Ten Commandments; to the Hebrew, the ten spheres of the Tree of Life. However the numeric symbolism of the tetractys also corresponds to the Hindu model of nine cobras around Brahma, the Egyptian Grand Ennead around Atum, and the Qabbalistic nine legions of angles around the Hidden God.”
It consists of ten points arranged as an equilateral triangle. As in the Lambda, the triangular form represents its divine nature.
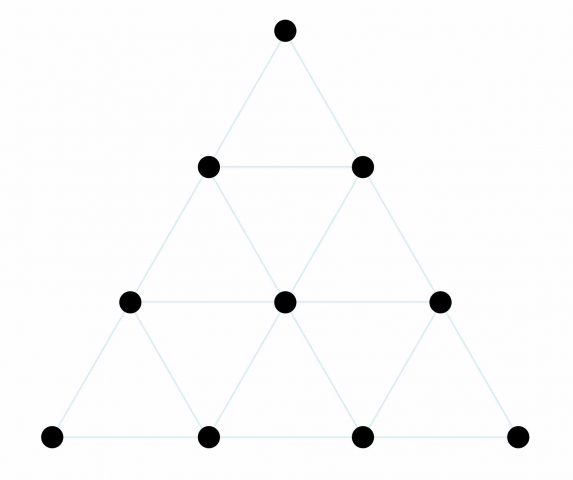
The tetraktys is a “cosmological model based on the completeness of ten points unfolding in four levels to describe the universal creating process.”3
The tetraktys is a representation of the Decad – the numbers 1-10. It consists of 4 levels.
Note that 10 = 1 + 2 + 3 + 4.
The four levels represent the increasing densities of the 4 elements: earth (most dense), water, air, and fire (least dense).

The four levels also define the unfolding of space: the point, line, surface & volume: 1D, 2D, 3D and 4D.
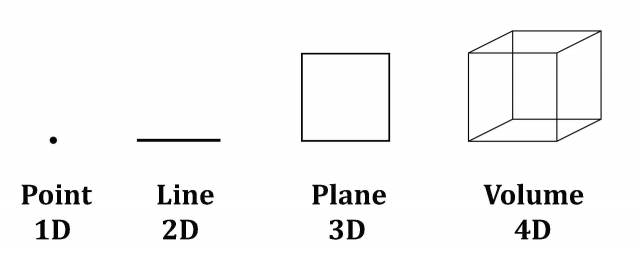
This symbol is a metaphor for the way the archetypes of 1-10 unfold and clothe themselves with matter to manifest as nature’s visible patterns.
The tetraktys also holds the geometry of all five Platonic solids and the geometry of music. The numbers 1, 2, 3, and 4 encapsulate the fractional lengths of a vibrating string that produces the natural 7-tone musical scale: the octave (1:2), the double octave (1:4), the fourth (3:4) and the fifth (2:3). These are the harmonics that govern creation.
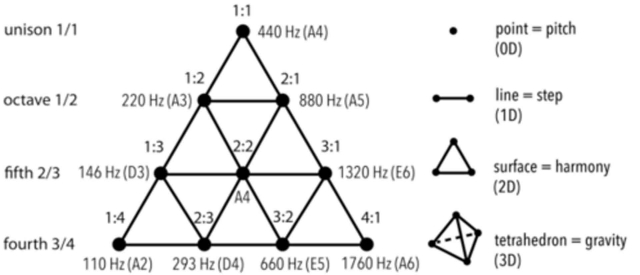
The four levels also refer to the different perspectives of viewing any subject:

The four levels also refer to the four levels of knowing. They are:
- Sense data – ‘a confusing multiplicity of sights, sounds, feelings, smells, tastes and so on, pure difference’.
- Recognition – to acquire information
- Knowledge – the ability to recognize or distinguish and agree shared knowledge in order to establish truth.
- Wisdom – the disciplined fourth stage – the distillation of knowledge that refers to seeking the essential values which offer unifying wholeness.
Michael Schneider tells us, “The Pythagoreans realized that the Tetraktys represented an ensemble, a unity, a summing up of the whole that comprehended the completeness of mathematics and the archetypes that manifested themselves as the visible forms of the world.”

John Michell writes, “The Tetractys, the triangular form of the number 10, had the same significance to the Pythagoreans as the Tree of Life diagram has in Jewish mysticism (discussed in Article 6), both being accounted symbols of the universe, and the numbers 1 to 4 of which it is composed were said to be at the root of all creation.”
The Sacred Alphabet of the Pythagoreans
As a bonus section I will include an interesting assessment of the Sacred Pythagorean alphabet as described by Anne Macaulay in Homage to Pythagoras – The Pythagorean Definition of God.
Macaulay writes: “The Pythagoreans were unique in that they used the letters of the alphabet both as numerals (a feature common to all early alphabetic usage) and as geometric symbolism. Geometry in the well-known Pythagorean form is unique to the Greek Pythagoreans, so the next thought was whether the alphabet in a pre-literary sacred form was at the root of the megalithic culture. This idea makes the alphabet into a numero-geometric system which was also used for the basic elements of speech (vowels and consonants). If there has been an earlier sacred form, then it would not have been used to write vulgar language.
The sacred alphabet is an ancient system in which the numerals and geometric elements were represented by geometric symbols; to each of these signs a single sound (vowel or consonant) was added, in order to create names appropriate to their significant geometric figures. Here we assess the name of the God Apollo. Apollo represented the transcendent principle. This was in contrast to Dionysus – the Divine Principle in its genesis or becoming. Dionysus must be torn to pieces and sacrificed by the Titans, then reassembled and remembered. This is Apollo – that which has been transformed
A = a circle with diameter ten units (alpha = 1st letter)
P = a circle with circumference 17 units (pi = 17th letter)
O = a circle with circumference 16 units (omicron = 16th letter)
L = a rectangle with sides 3 x 4 (lambda = 12th letter)
N = a circle with circumference 14 units; its diameter is 4.4545, using pi = 22/7 (nu = 14th letter)




The numero-geometric values of the letters of the name Apollo form a concise and well-defined figure. Thus we can conclude that Apollo is the name derived through the sacred numero-geometric alphabet from a geometric figure, which was itself derived from astronomical observations of the circumpolar stars and the moon. The secondary dimensions of the figure are the set of proportions of the scale and basic acoustic laws.
Apollo, the god derived from a geometric figure is no deified hero nor an archetypal godlet, but a synthesis of observed facts about the relation of the stars, the moon and the sun to earth; it is a time piece and a calendar; it is a statement of the laws of the heavens in terms of geometrical and mathematical elements which themselves exhibit absolute laws; and these laws also apply to music.
The existence of this stream of Apollo wisdom explains the problem of why the later teachers, Socrates and Plato, etc. were known as Pythagoreans in their day but there was no direct intermediary who could have passed Pythagoras’ teaching on to them. The relationship is that they were all teaching aspects of the Apollo wisdom in public.
Perhaps the most important message from Apollo to us today is to become aware again in practice of the harmony which pervades all being.”
Conclusion
We have taken a look at Number through the lens of the ancient esoteric philosophers and noticed the importance of numbers as symbols representing the qualities of consciousness – consciousness that shapes our personal reality, cosmic consciousness that shapes the universe, and the combination and collaboration of the two as one unified whole.

- Michell, John, The Dimensions of Paradise, pg. 49
- Olsen, Scott, The Golden Section: Nature’s Greatest Secret, Walker Books, 2006
- Schneider, Michael, A Beginner’s Guide to Constructing the Universe
Recent Comments