Return to Free Library

Return to Number Menu

Previous Article                                                                         Next Article

This article will round out our discussion of triangles by discussing Golden and Pythagorean triangles.

Golden triangles will be discussed again in the section about the Pentad (Articles 52-59).

Golden Triangles

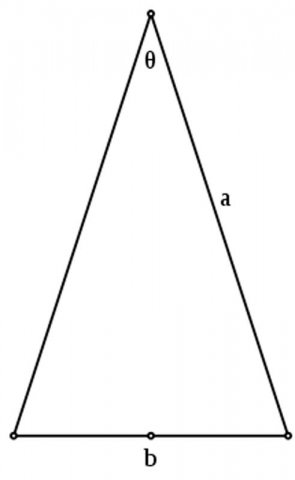
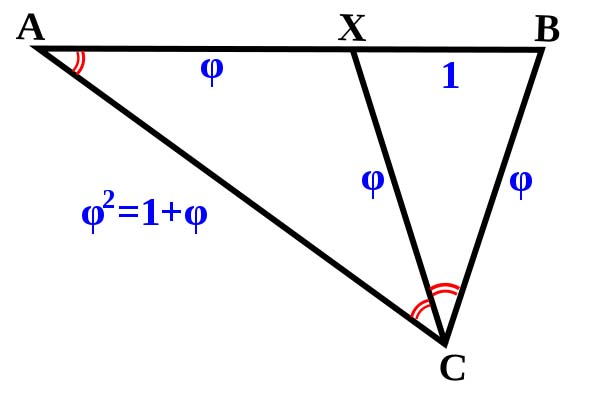
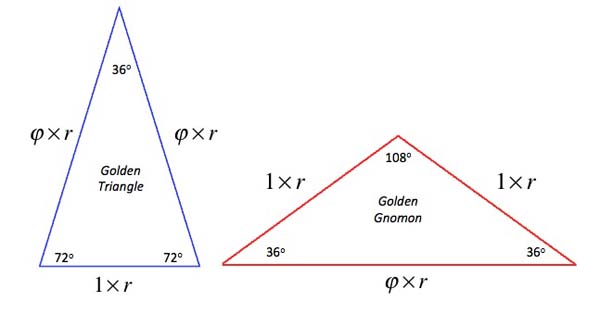
A golden triangle, or sublime triangle, is an isosceles triangle in which the duplicated side is in the golden ratio to the distinct side.

In the case below, the ratio a:b is equivalent to the golden ratio φ.

This means if b = 1 then a = 1.618…

Also, b:a :: a: (a+b)

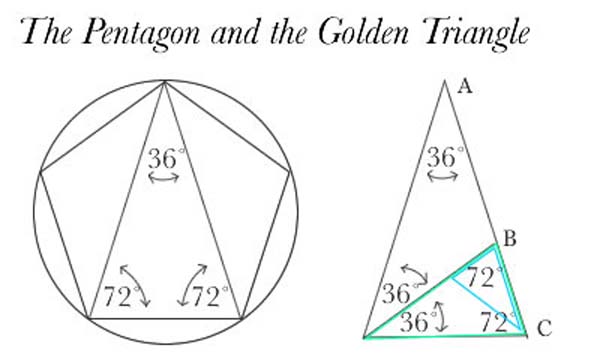
The golden triangle is also the shape of the triangles found in the points of pentagrams. The vertex angle in this case is 36º and the base angles are 72º.

36 + 72 + 72 = 180.

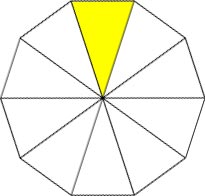
The golden triangle can also be found in a decagon (10-sided polygon) by connecting any two adjacent vertices to the center.

The golden triangle is also the only triangle to have its three angles in a 2:2:1 proportion.

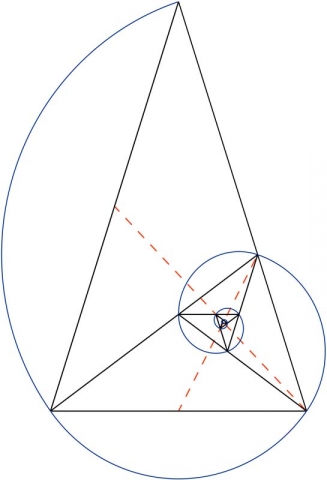
The golden triangle is also used to form a logarithmic spiral, as seen below on the far right. “By bisecting the base angles, a new point is created that in turn, makes another golden triangle. This bisection process can be continued infinitely, creating an infinite number of golden triangles. A logarithmic spiral can be drawn through the vertices.”1

The Golden Gnomon

The Golden Gnomon is closely related to the golden triangle. The golden gnomon is the obtuse triangle in which the ratio of the length of the equal (shorter) sides to the length of the third side is the reciprocal of the golden ratio.

The Golden Gnomon is also the only triangle to have its three angles in a 1:1:3 proportion.

The acute angles are 36 degrees. The apex angle is 108º. (36 + 36 + 108 = 180)

The golden gnomon is the “roof” of a pentagon, as seen below.

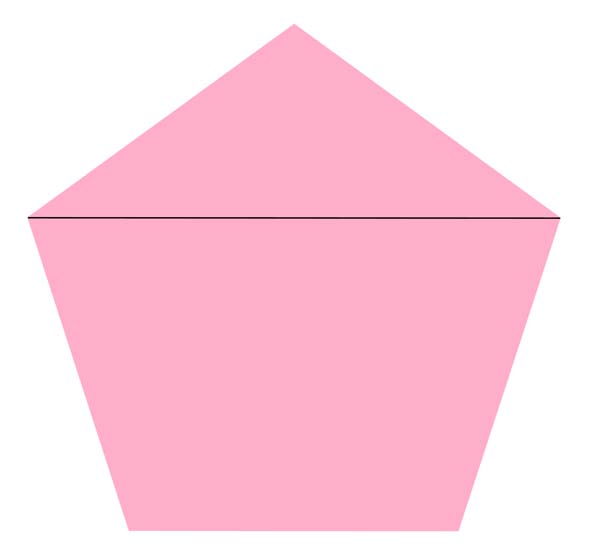
“The golden triangle has a ratio of base length to side length equal to the golden section, whereas the golden gnomon has the ratio of side length to base length equal to the golden section.”2

A golden triangle can be bisected into a golden triangle and a golden gnomon. The same is true for a golden gnomon.

Golden triangles and gnomons are found in the nets of three Kepler-Poinsot solids: the the small stellated dodecahedron, the great stellated dodecahedron and the great dodecahedron.

Great Stellated Dodecahedron (golden triangle):

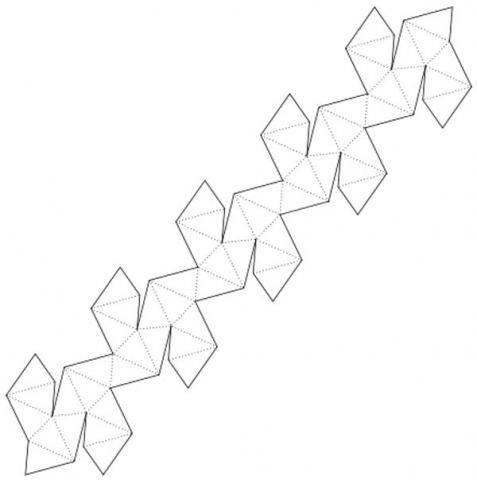
Small Stellated Dodecahedron (golden triangle):

Great Dodecahedron (golden gnomon):

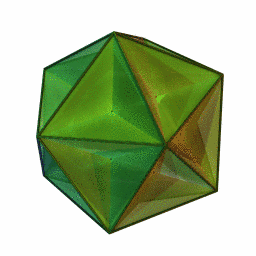
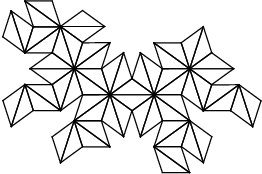
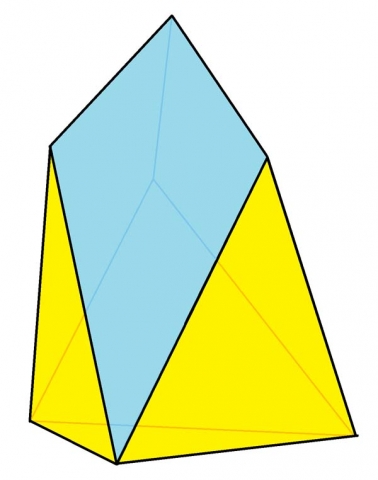
The golden triangle also shows up in the 7-sided figure the Chestahedron, discussed in Article 67.

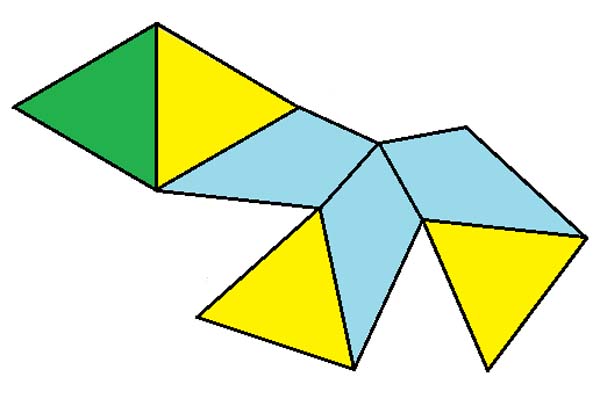
Square Root Spiral

The square root spiral is also called the Pythagorean spiral, or Spiral of Theodorus.

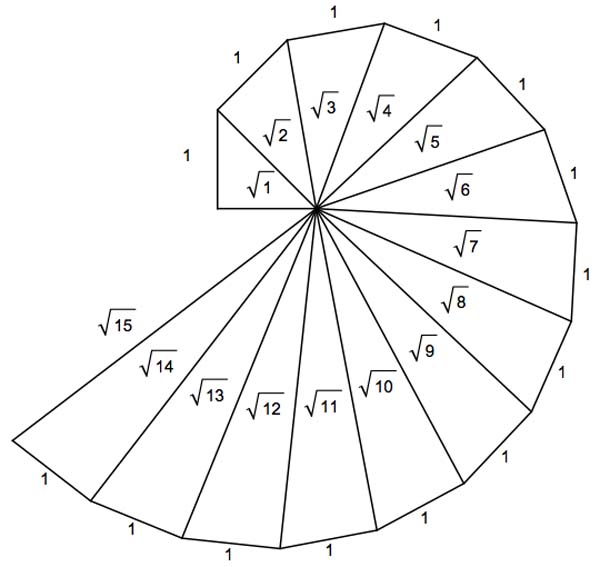
It is composed of contiguous right triangles and was first constructed by Theodorus of Cyrene (5^th century BC).

By starting with an isosceles right triangle with legs of length 1, we can build adjoining right triangles whose hypotenuses are of length √2, √3, √4, √5, √6…etc.

“In 1958, Erich Teuffel proved that no two hypotenuses will ever coincide, regardless of how far the spiral is continued. Also, if the sides of unit length are extended into a line, they will never pass through any of the other vertices of the total figure.”3

The Spiral of Theodorus approximates the Archimedian spiral seen below.

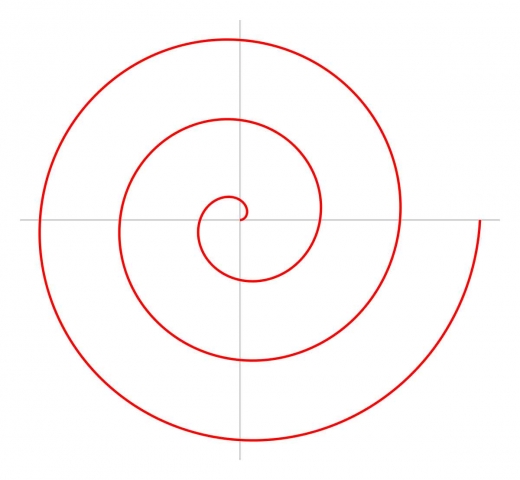
“Just as the distance between two windings of the Archimedian spiral equals mathematical constant pi, as the number of spins of the spiral of Theodorus approaches infinity, the distance between the two consecutive windings quickly approaches pi.”4

After only the 5^th winding, the distance is a 99.97% accurate approximation to pi.

Reference Construction Lesson # 25: The Spiral of Theodorus.

The “Sacred Triangle” or Pythagorean Triangle

‘Sacred’ in this case means fixed or permanent symbolizing the fused sacral bones of the spine which makes possible the stable, seated posture.

Keith Critchlow writes, “A Pythagorean triangle is a three-sided figure with one angle a right angle of 90 degrees and with side lengths which are whole numbers; the third number can be ascertained if the other two are given.”

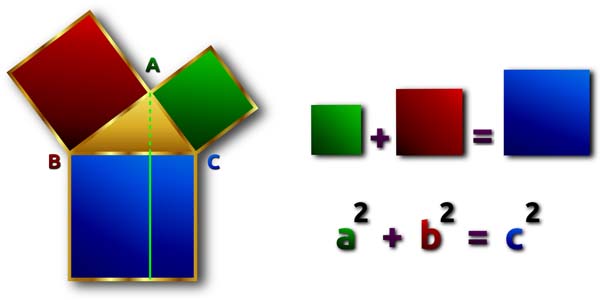
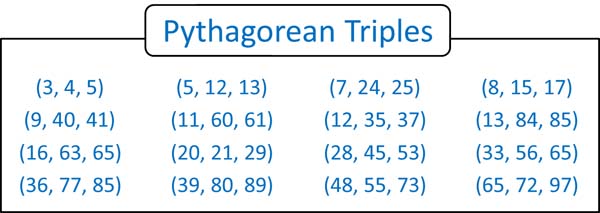
Pythagorean Triples

Pythagorean triples are integer solutions to the Pythagorean Theorem: a2 + b2 = c2.

These are any set of three numbers that satisfy the Pythagorean Theorem.

Using the above diagram the way to determine a subset of Pythagorean triplets is as follows:

• Every odd number is the side a of a Pythagorean triplet.
• The b side is (a² – 1)/2.
• The c side is b + 1.

There are an infinite number of Pythagorean triplets, because there are an infinite number of odd numbers.5

However, there are Pythagorean triplets in which the a side is an even number. In this case, solutions can be generated as follows:

• Every even number is the a side of a Pythagorean triplet.
• The b side of such a triplet is (a/2)² – 1.
• The c side is b + 2.

Pythagorean Triangles and Electromagnetism

As illustrated in the previous article 30, there is an intimate relationship between sine waves, right-angled triangles and spiraling helices.

The right-angle in Pythagorean triangles are important symbols of electromagnetism as the two linear waves are oriented to each other at 90 degrees.

The opposite and adjacent vectors at 90 degrees are seen as the electric and magnetic waves.

The hypotenuse signifies the path of no resistance between the two as angular momentum.

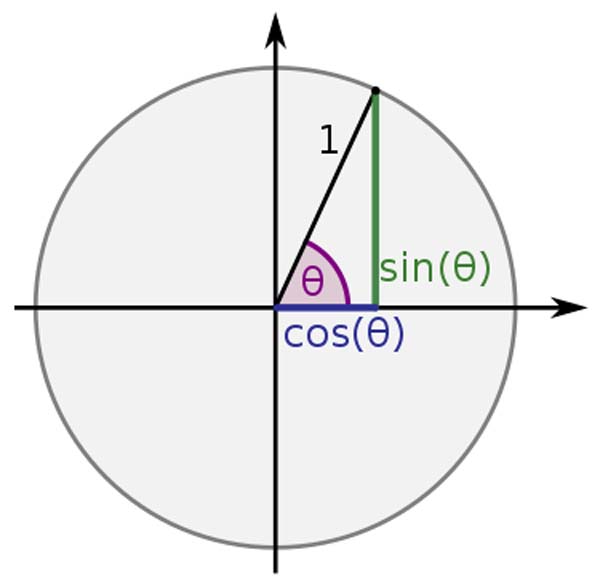
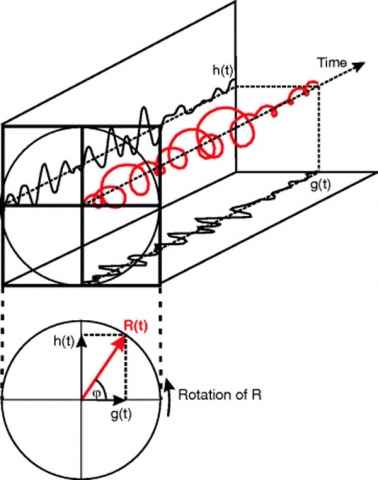
We will now take a look at five specific Pythagorean triangles.

3-4-5 Triangle

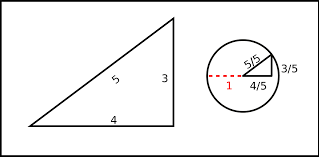
The 3-4-5 triangle is the only right-angle triangle whose sides are in an arithmetic progression (each successive term is created by the addition of a common difference:

3 + 1 = 4 and 4 + 1 = 5

Area = 6

Semi-perimeter = 6

Perimeter = 12

Enclosed circle = diameter 2

“A length of twelve units, twelve also having a zodiacal and duodecimal significance, is the minimum measured length which can be triangulated into a three, four, five pattern to give a perfect 90º angle.”6

“The first basic triad three, four, and five, also gives us a particularly interesting conjunction of the two main significant numbers that occur in the shaman cosmology – seven from its first two parts (3 + 4 = 7) and nine from its last two parts (4 + 5 = 9).”7

3 + 4 + 5 = 12

3 x 4 x 5 = 60

12 + 60 = 72

12 x 60 = 720

“12 and 60 are at the root of the numerical code that supplies all the dimensions of the New Jerusalem.”8

The ‘New Jerusalem’ refers to building the cosmic temple upon Earth. This Cosmic temple refers to creating an earthly society that reflects the harmony and unity of the cosmos. Thus, the earthly cosmic temple means rebuilding society into one in which harmony, justice, peace, compassion and wisdom prevail.

Their sum is 72 – the preeminent number of the Sacred Number Canon.

Their product is 720 – the number of Truth in Gematria and the number of the tetrahedron.

3, 4, and 5 multiplied by 720 = 2160, 2880, and 3600 respectively.

2160 – The number of the cube

2880 – Twice the number of the octahedron & star tetrahedron (1440)

3600 – The number of the icosahedron

Reference Construction Lesson # 26: Pythagorean Triangles

5-12-13 Triangle

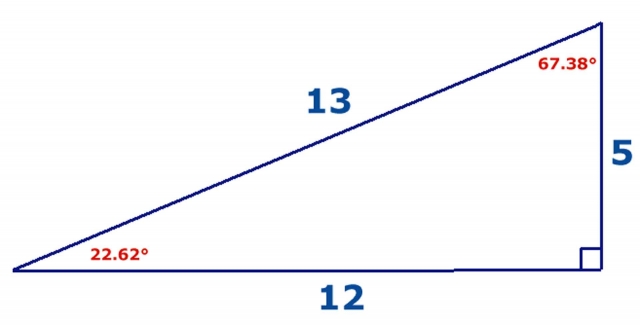
Area = 30

Perimeter = 30

Enclosed circle diameter = 4

The 5-12-13 triangle is the subject of much research by Robin Heath particularly his book Sun, Moon & Stonehenge.9

The 5-12-13 triangle is used in some ancient stone circles to find the exact number of lunar months in the solar year.

12 is traditionally a solar number; 13 a lunar number.

“Dividing the 5 side into its harmonic 2:3 [the perfect fifth] gives a new length, 153, or 12.369, the number of full moons in a year (99.999% accuracy).”10

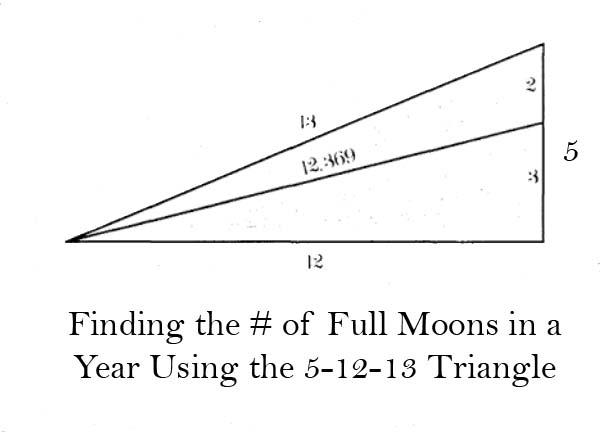
You can see, the Moon encodes the first two Pythagorean Triples.11

8-15-17 Triangle

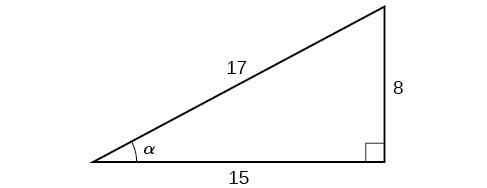
Area = 60

Perimeter = 40

Enclosed circle diameter = 6

7-24-25 Triangle

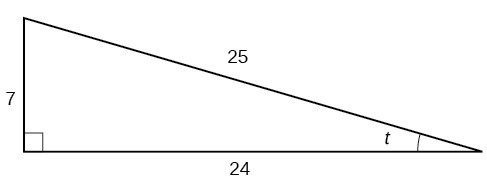
Area = 84

Perimeter = 56

Enclosed circle diameter = 6

12-35-37 Triangle

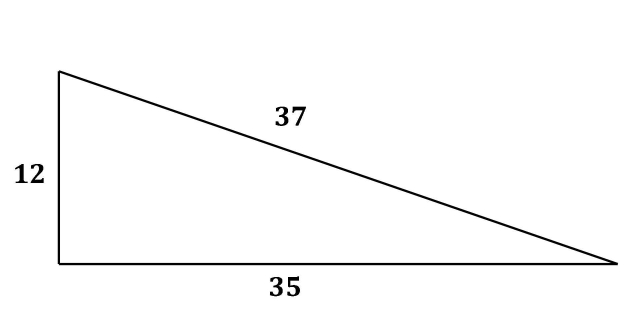
The 12-35-37 triangle is the most exploited triangle by Neolithic builders according to Professor Alexander Thom.

After surveying 600 sites, Professor Thom found that ancient stone circles were built around Pythagorean triangles.

He said, “[Megalithic man] had an extensive knowledge of practical geometry, and used the 3, 4, 5 right-angle triangle extensively. He also knew the 5, 12, 13 right-angle triangle, the 8, 15, 17 and the 12, 35, 37. There is a suspicion that he also knew the 9, 40, 41. He had in addition discovered many other triangles with integral sides that satisfied very closely the Pythagorean relation. These triangles were used in a peculiar geometry, in which he constructed rings, set out in stone, or various shapes: circular, egg-shaped, elliptical, etc.”12

Source: Quadrivium, page 113

“A statistical analysis of the sites shows that they were so carefully erected that we can from them deduce:

1. the inclination of the ecliptic
2. the inclination of the lunar orbit
3. the mean amplitude of the lunar perturbation and
4. the mean lunar parallax

with an accuracy better than one arc minute…”13

Nested Pythagorean Triangles

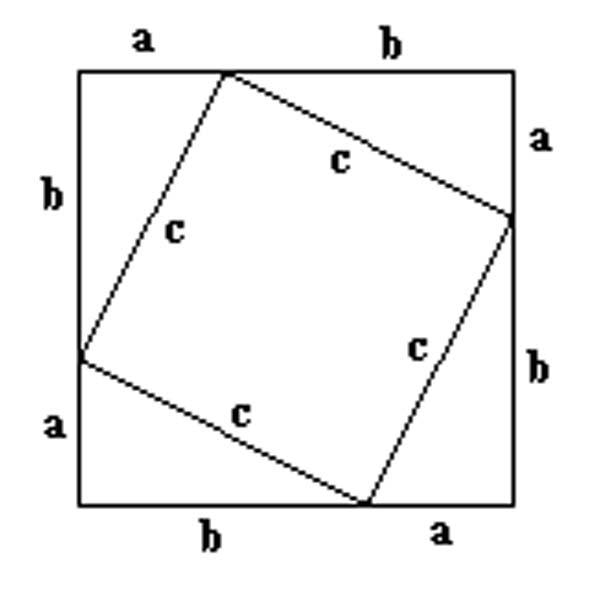
In the following diagram:

• The area of the entire square is (a + b)²
• The area of each triangle is ½ ab.
• The area of the inner square is c²
•  

Now look at a more complex example below.

The middle blue square in the center is a unit square.

The rest are Pythagorean triangles.

Plato’s series:

Smallest: 3-4-5; Middle: 8-15-17 Largest: 12-35-37

Proclus, in his commentary to the 47th Proposition of the first book of Euclid’s Elements, describes it as follows:

“Certain methods for the discovery of triangles of this kind are handed down, one which they refer to Plato, and another to Pythagoras. (The latter) starts from odd numbers. For it makes the odd number the smaller of the sides about the right angle; then it takes the square of it, subtracts unity and makes half the difference the greater of the sides about the right angle; lastly it adds unity to this and so forms the remaining side, the hypotenuse.
…For the method of Plato, argues from even numbers. It takes the given even number and makes it one of the sides about the right angle; then, bisecting this number and squaring the half, it adds unity to the square to form the hypotenuse, and subtracts unity from the square to form the other side about the right angle. … Thus it has formed the same triangle that which was obtained by the other method.”14

Pythagoras’s Series:

Smallest: 3-4-5; Middle: 5-12-13; Largest: 7-24-25

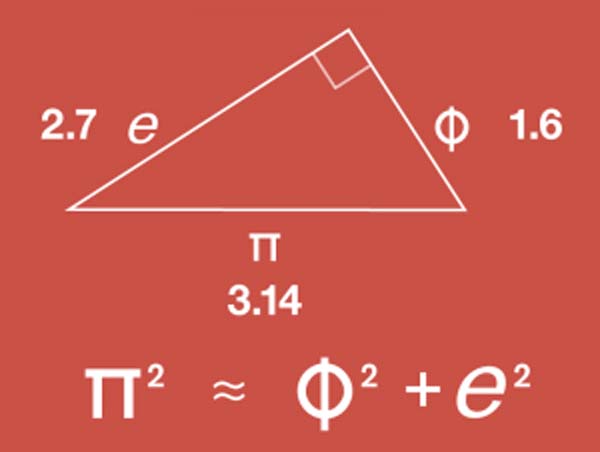
Pythagorean Triangle, π, φ, & e

Here we see a Pythagorean triangle using the constants of pi (π), phi (φ) and e to one decimal place.

Conceptually:

• π = circular perimeter
• φ = expansion
• e = growth

If a² + b2 = c2 then 2.72 + 1.6² = 7.29 + 2.56 = 9.85 √9.85 = 3.14…

Combined, these three constants appear to create a symbolic space within a rotation.

This gives us a glimpse of the interconnectedness of the physical constructs of our universe.

This is also interesting in light of the disputed value for pi discussed briefly in Article 12. A new value of pi based on the golden ratio further supports the interconnectedness of our universe.15 This new value of pi is said to be:

π = 4/√φ or 3.144605511…

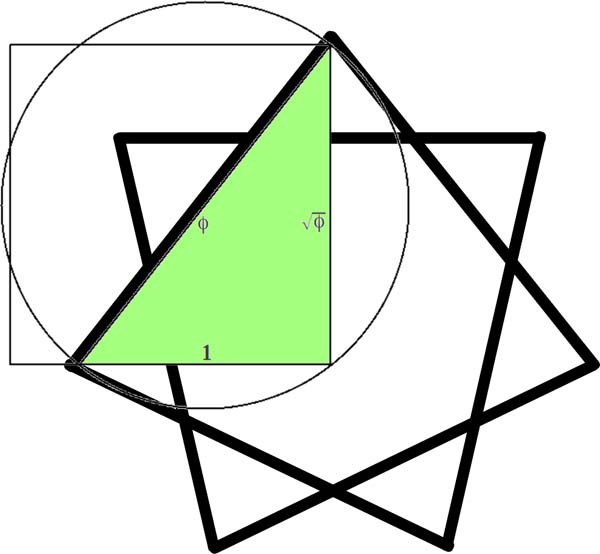
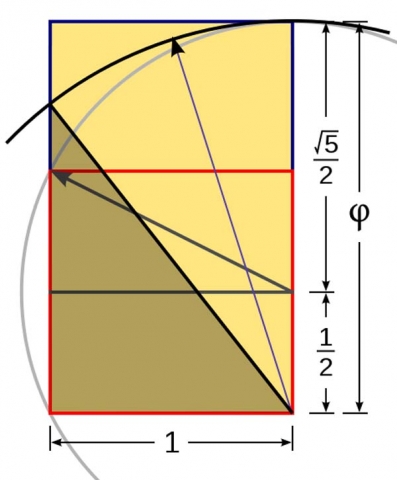
The Kepler Triangle

The Kepler triangle is a right triangle with edge lengths in geometric progression (each term is created by the multiplication of a common ratio). The ratio of the edges of a Kepler triangle is linked to the golden ratio: φ = (1 + √5)2

The Kepler triangle, is of course, based on the Pythagorean theorem a² + b² = c².

1 + Phi = Phi² (1 + 1.618….= 2.618…)

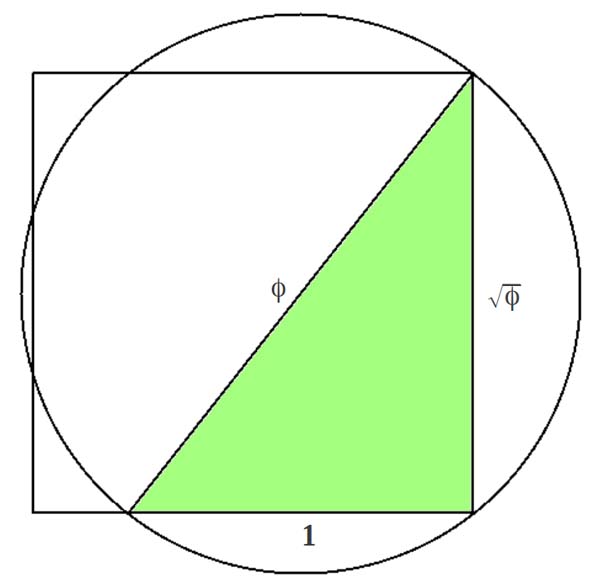
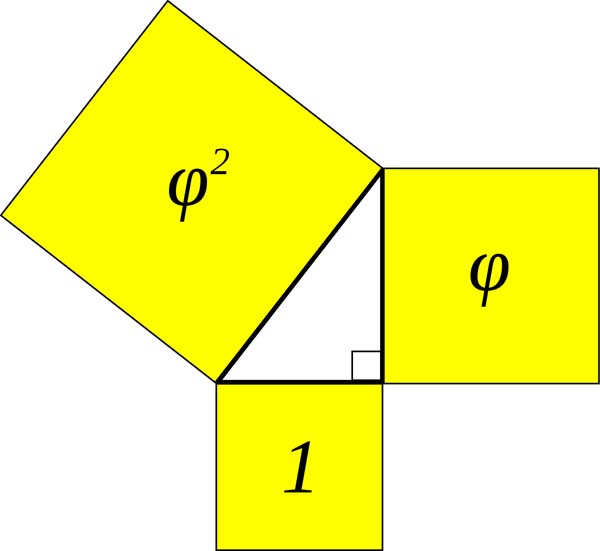
This is a right triangle based on the golden ratio phi.

It has an angle of 51.83º (or 51º50′) and a cosine of 0.618.

This angle is used in the Great Pyramid of Egypt. The Great Pyramid is composed of two of these Kepler triangles back to back.

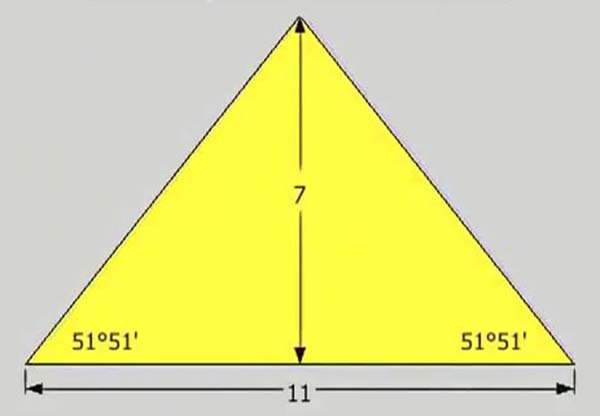
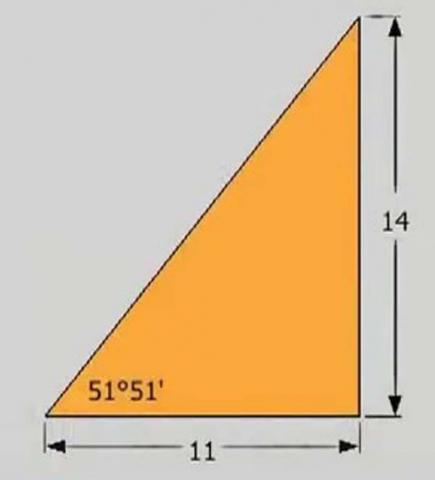
The Kepler triangle is the only right-angle triangle whose sides are in a geometric progression:

√φ x φ = 1 and

1 x φ = φ

The Kepler Triangle and Squaring the Circle

Take any Kepler triangle with sides a, a√φ, aφ.

The circle that circumscribes it and a square with side equal to the middle-sized edge of the triangle will have perimeters of circle and square equal up to an error less than 0.1%.

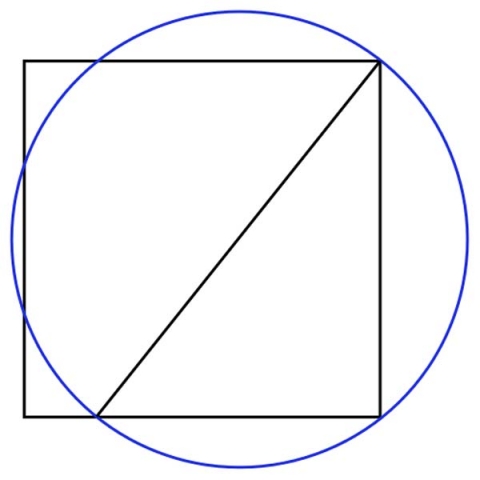
This would mean π = 4√φ as we saw above.

This is chalked up to a mathematical coincidence. Yet the verification and proofs of this are discussed extensively by Kevin Barrett in The Great Pi Conspiracy.

We are not saying he is right, but we are not saying he is wrong. It is a very interesting discussion.

The Kepler triangle is also found in the structure of the heptagram, the seven-pointed star.

Reference Construction Lesson # 27: Kepler Triangles

1. https://en.wikipedia.org/wiki/Golden_triangle_(mathematics)
2. ibid.
3. https://en.wikipedia.org/wiki/Spiral_of_Theodorus
4. ibid.
5. Ross, Kelly L, Pythagorean Triples, http://www.friesian.com/pythag.htm
6. Critchlow, Keith, Sacred Geometry: Philosophy & Practice, Thames & Hudson, 1982
7. ibid.
8. Michell, John, The Dimensions of Paradise, Inner Traditions, 2^nd ed, 2008
9. Heath, Robin, Stonehenge: The Marriage of the Sun and Moon, http://cura.free.fr/decem/06heath.html
10. Martineau, John, A Little Book of Coincidence in the Solar System, Walker Publishing Company Inc, 2001
11. http://joedubs.com/pythagorean-triples/
12. Thom, Alexander, Megalithic Lunar Observations, Oxford University Press, 1971
13. Ginenthal, Charles, Pillars of the Past, Volume Four, 2015
14. https://en.wikipedia.org/wiki/Pythagorean_triple
15. Wollum, Mark, The Great Pi Conspiracy, 5 February 2015, Veterans Today, https://www.veteranstoday.com/2015/02/05/pi/