This article will continue part 2 of our 3-part discussion of triangles.

Three types of Triangles: Equilateral, Isosceles, Scalene
-
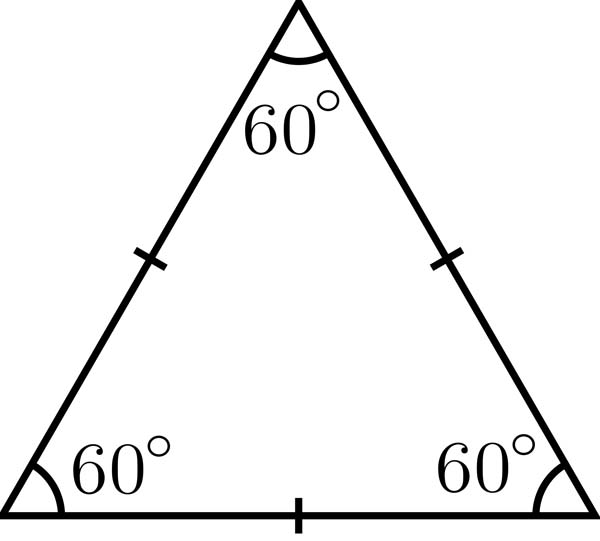
The Equilateral Triangle
The equilateral triangle brings forth the birth of surface and structure.
It remembers its source in the Monad by having equal sides and equal angles (60 degrees).
The relationship of the height (altitude) of the triangle to the distance between the two centers is √3:1. We saw this in the Ad Triangulum method in the last article.
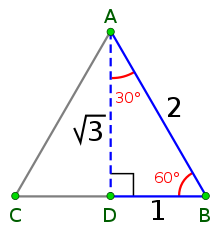
Ad Triangulum refers to the ratio 1 : 2 : √3.
From the Vesica Piscis more triangles can be generated by the natural points of the equilateral triangle. (See page 45 M.S.) This means the equilateral triangle is a self-similar fractal shape.

The Decomposed Triangle
One can geometrically decompose or subdivide a triangle into smaller triangles that diminish by the same root-3 relationship.
The lines meet at 120 degrees – (the center angle between two points).
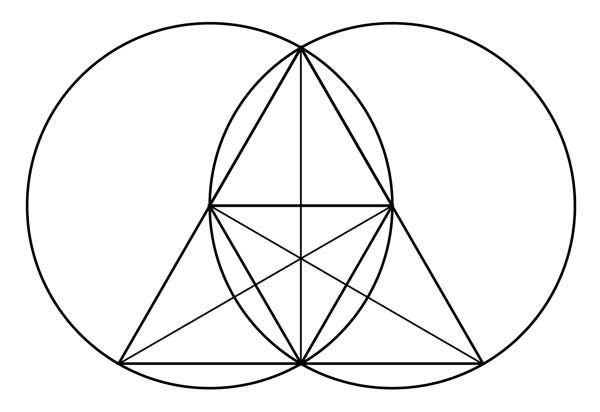
This can be seen as lines of force in creation in nature.
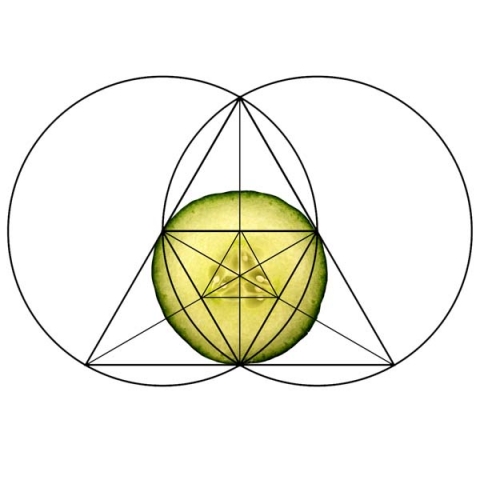
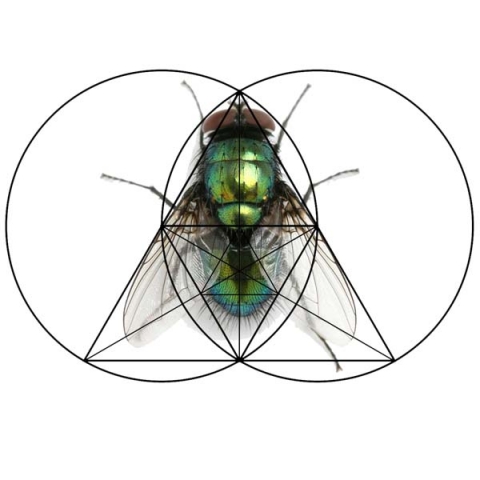
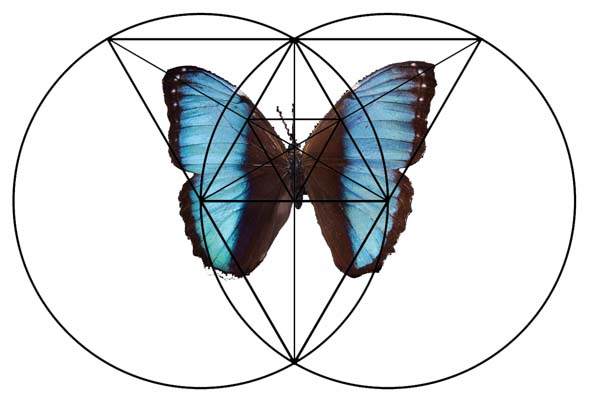
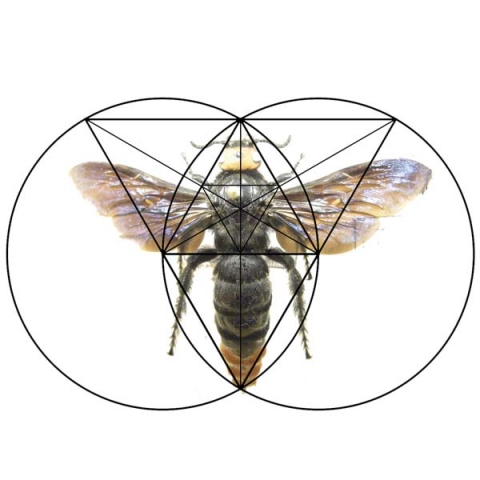
See the geometry of a cucumber, melon, bell pepper, butterfly, flower, and fly fit within the decomposed triangle. These are a few examples among thousands.
Remember, all matter is built off invisible force lines of standing waves of geometry. Geometric analysis of lifeforms can help us find the underlying pattern.
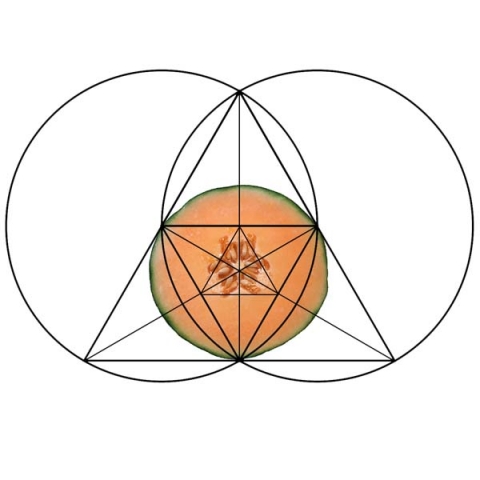
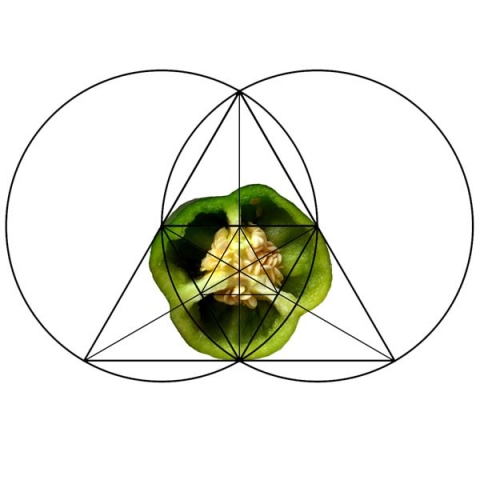
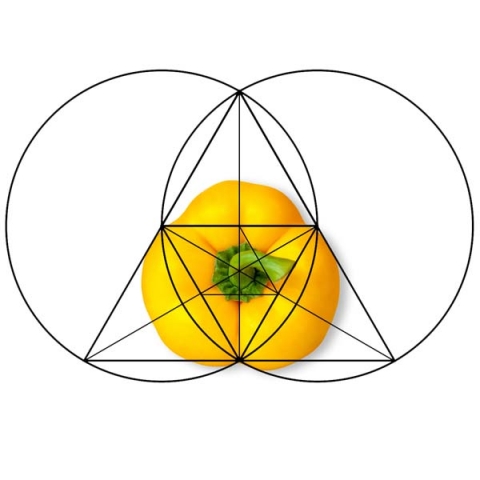
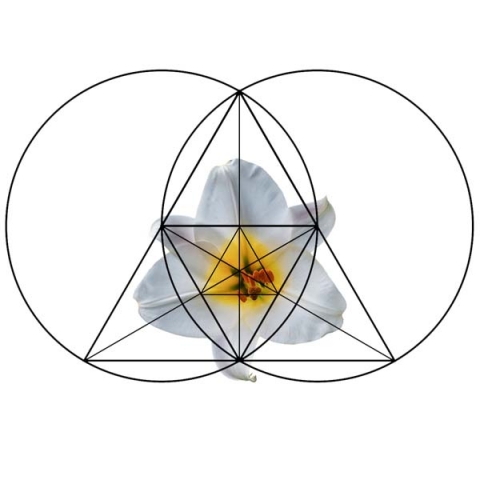
-
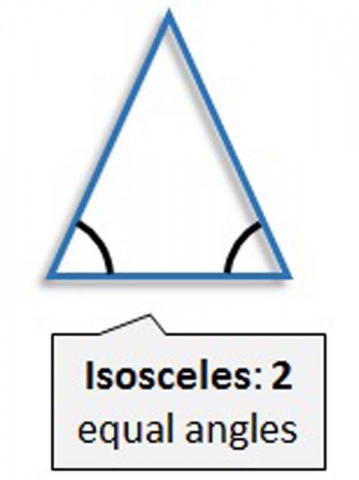
Isosceles Triangle
An isosceles triangle has two equal sides and two equal angles.
-
Scalene Triangle
A scalene triangle has no equal sides and no equal angles.
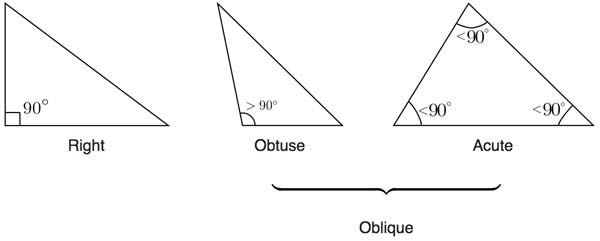
Three types of Angles
-
Acute Triangle
All angles are less than 90.
- Right Triangle
Has one right angle (90).
Two lines form a right angle when the adjacent angles are equal.
- Obtuse Triangle
Has one angle more than 90.
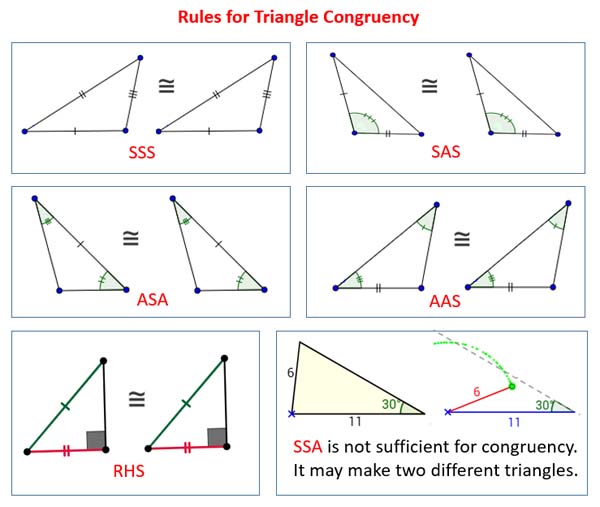
Congruent Triangles
Side Side Side Postulate (SSS)
If three sides of one triangle are congruent to three sides of another triangle, then these two triangles are congruent.
Angle Side Angle Postulate (ASA)
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, the two triangles are congruent.
Side Angle Side Postulate (SAS)
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.
Angle Angle Side Postulate (AAS)
If two angles and the non-included side of one triangle are congruent to two angles and the non-included side of another triangle, then these two triangles are congruent.
Trigonometric Functions and Right Triangles
Reference Construction Lesson #23: Trigonometry Review
In right triangles, the trigonometric ratios of sine, cosine and tangent can be used to find unknown angles and lengths of unknown sides.
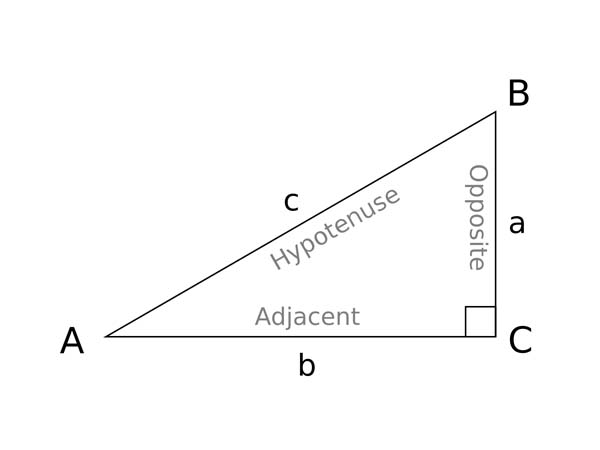
Hypotenuse – the longest side of a right-angled triangle; or side opposite the right angle
Opposite side – side opposite to the angle we’re interested in
Adjacent side – the side in contact with the angle we’re interested in
Sine and Cosine are ratios. They represent relationships.

Sine – the sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse
sin A = opposite side/ hypotenuse
Cosine – the ratio of the length of the adjacent side to the length of the hypotenuse
cos A = adjacent side/hypotenuse
Tangent – the ratio of the length of the opposite side to the length of the adjacent side
tan A = opposite side/adjacent side
Cotangent
cot A = adjacent side/opposite side
Secant
sec A = hypotenuse/adjacent side
Cosecant
csc A = hypotenuse/opposite side
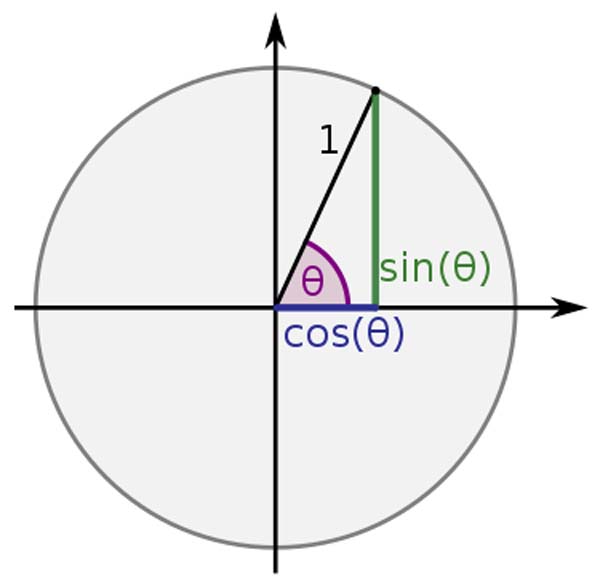
Sine and Cosine
Sine and cosine represent a unit circle projected onto a time axis and rotated.
Periodic repetition occurs through continuous cycles. Sine has no beginning or end.
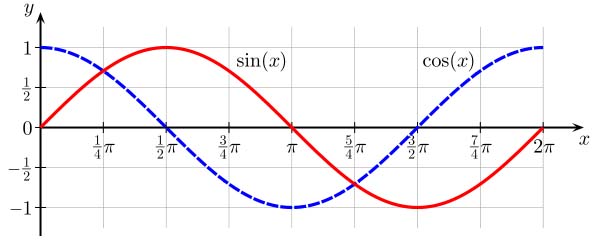
Sine is the orthogonal projection of the rotated unit circle.
Cosine has similar relation to the unit circle, just 90 degrees out of phase.
As we’ve seen, sine and cosine are orthogonal projections of a rotated Unit circle.
This means sine and cosine are orthogonal 2d projections of the 3D unit helix.
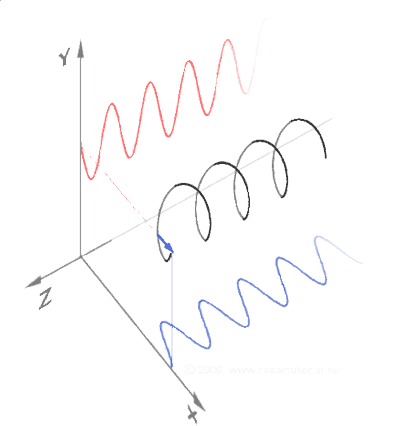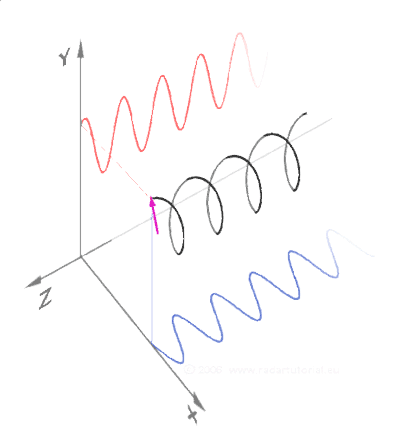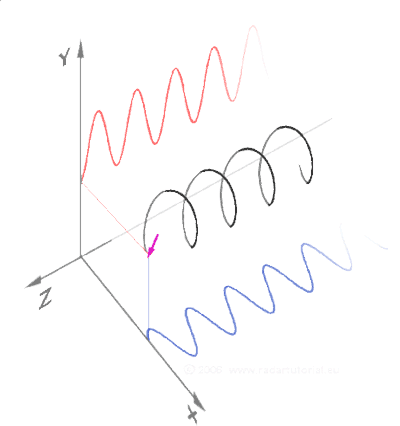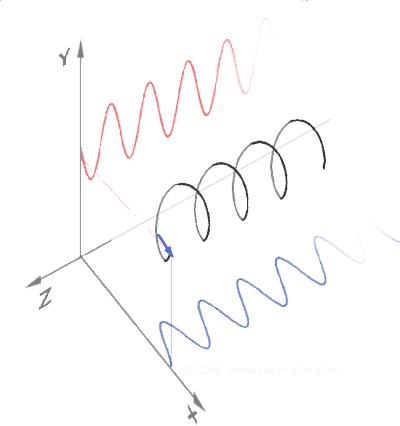
Electromagnetic Waves and Right Triangles
The importance of the following imformation lies in the ability to see how right triangles are intimately related to waves. According to the esoteric stream of knowledge all matter is made of light. Light is composed of electromagnetic waves. Thus all matter can be boiled down to a combination of wave structures. Right triangles and basic trigonometry can help us understand wave structure.
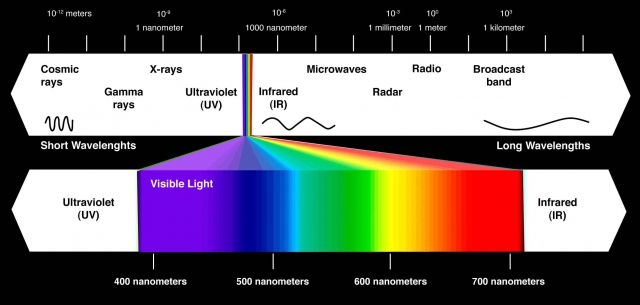
Sine and cosine in this sense tell us the ratio of the length of the magnetic axis to the electric axis. The hypotenuse represents angular velocity. The varying ratios or relationships will determine the type of wave and whether that wave falls into the visible spectrum of light or somewhere else such as the ultraviolet, x-ray, gamma ray, cosmic ray, infrared, microwave, radar, radio…spectrum.
Sine and cosine represent ratios of the electric axis to the magnetic axis. These ratios determine what type of wave it will be.
In standard diagrams of EM waves, two linear waves are oriented to each other at 90 degrees.
Credit: Drunvalo Melchizadek
A spiral may be traced to unify their alternating vectors through time.
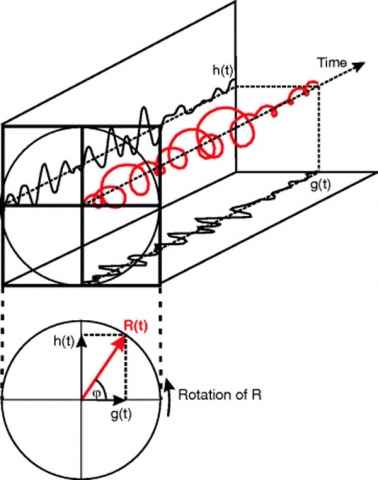
This triple relationship may be represented at any point in time by a right angled triangle.

The opposite and adjacent vectors at 90 degrees are traditionally distinguished as the electric and magnetic waves.
The image below shows how the electric and magnetic components are always at 90º to one another as they move through space.
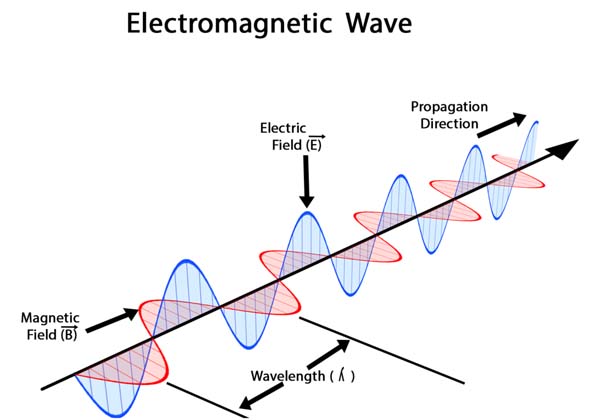
The hypotenuse would signify the path of no resistance between the two as angular momentum.
Wikipedia tell us that “angularmomentum is the rotational equivalent of linear momentum.” It is the quantity of rotation of a body, which is the product of its moment of inertia and its angular velocity.
Angular velocity is the rate of change of angular position of a rotating body (or how fast it is spinning).
The moment of inertia is “a quantity expressing a body’s tendency to resist angular acceleration. It is the sum of the products of the mass of each particle in the body with the square of its distance from the axis of rotation.”
This means the mass of each particle making up the matter is multiplied by the square of its distance from the axis (its distance squared). These products of each particle added together make up the total moment of inertia. Thus, the moment of inertia is dependent upon the mass of the particles and their distance from the center (or axis) of rotation.
The moment of inertia multiplied by the angular velocity equals the angular momentum.
Reference Construction Lesson #24 for the following two exercises.
- Equilateral Triangle in a Sphere
The circumference of an equilateral triangle in a sphere defines the octave.
The outer circumference (larger circle) is twice the diameter of its incircle. (2:1)
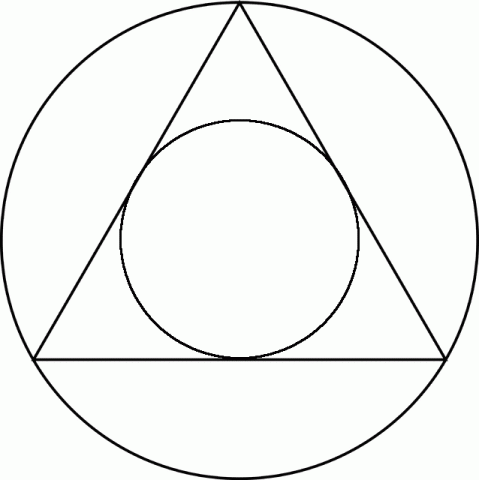
The area of the outer circle is three times that of the incircle (3:1). This is not an octave but is an interesting proportion of thirds, nonetheless.
-
Equilateral Triangle and the Golden Ratio
An equilateral triangle in a circle has many golden ratio proportions built in.
An equilateral triangle is placed in a circle. If a line is drawn horizontally using the midpoint of the side of a triangle, and then is extended to the circumference of the circle you will get a golden proportion.
Shown here, BC: AB :: AB : AC. This reveals a golden proportion.
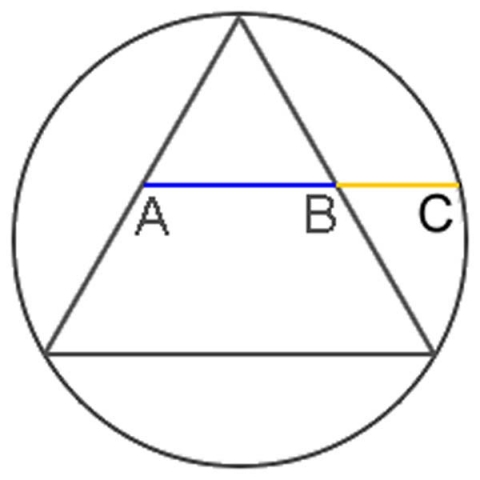
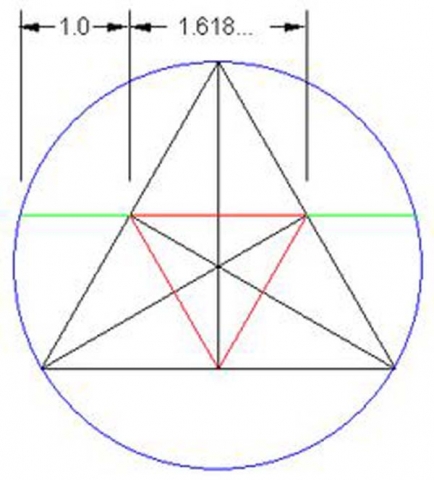
The key importance of this knowledge is to realize that wherever there is a rotating equilateral triangle or tetrahedron, there exists the golden ratio. The golden ratio itself is built into the rotating tetrahedron. The deeper significance is seen when the shape of the photon as a tetrahedron (or two tetrahdra back-to-back) is recognized. Photons spin as they travel through space. If photons are tetrahedrons, then as they spin through space (forming helixes) they create golden ratios in their wake.
The golden ratio is built into the spinning photon. The significance of the interrelatedness of the golden ratio, spiraling tetrahedron, photon, right triangles and the electromagnetic spectrum deserves deeper contemplation.
Next we see three more diagrams illustrating the golden proportion.
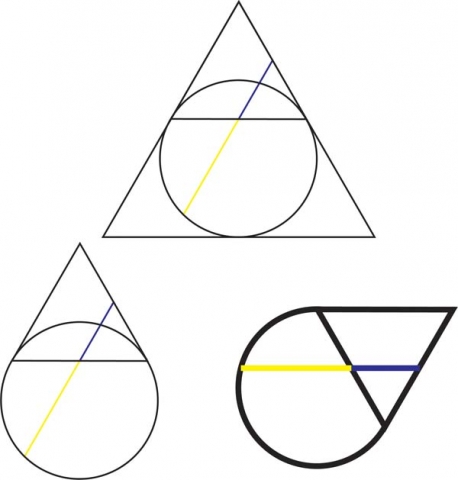
These three diagrams show the circle within the triangle, rather than the triangle within the circle. These involve drawing a chord across the circle with endpoints on the midpoint of the triangle’s sides. Then a line is drawn parallel to the triangles side that bisects the chord.
The length of the yellow line to the blue line shows the golden proportions.
We will finish with a look at a beautiful piece of art regarding the triangle and the circle.
The Eye of Providence
The Eye of Providence on the Chruch of Saint Mary Magdalene (La Maddalena) in Venice, Italy shows the area of the triangle and its interwoven circle.


In this case, the area of the triangle and the area of the circle are equal. Thus, they are harmonized.

Recent Comments