In this article we will discuss one aspect of the Triad regarding the Platonic Solids and show the significance of triangles regarding these solids.
“What do all structures have in common that allows their coherence? Triangles. At the root of all stable complexes is nature’s only self-stabilizing pattern.”1

Convex Deltahedra (See page 155 Quadrivium)
Convex deltahedra are volumes made from only equilateral triangles.
There are eight total.
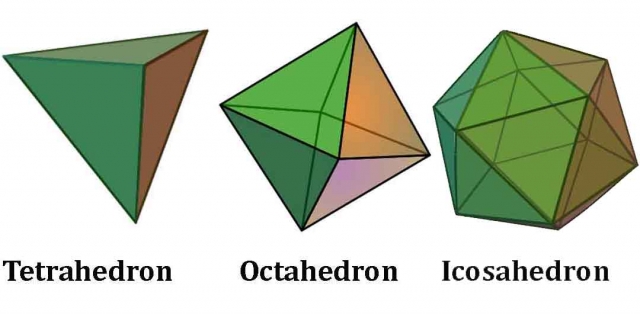
“Remember that only three systems can be made out of regular triangles: tetrahedron, octahedron, and icosahedron. These are the ‘three prime structural systems of the Universe.”2
There are 3 regular solids:
- tetrahedron (4 sides)
-
octahedron (8 sides)
- icosahedron (20 sides)
There are 5 irregular solids:
- triangular bipyramid – 2 tetrahedra glued back-to-back (6 sides)
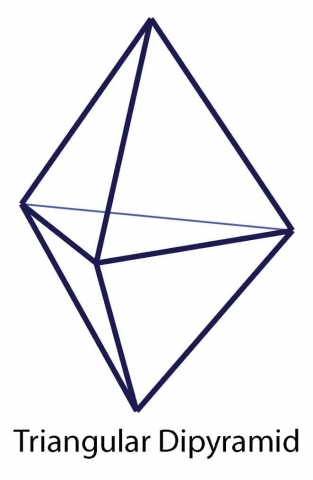
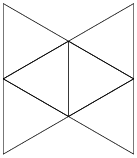
- pentagonal bipyramid – two pentagonal pyramids glued back-to-back (10 sides)
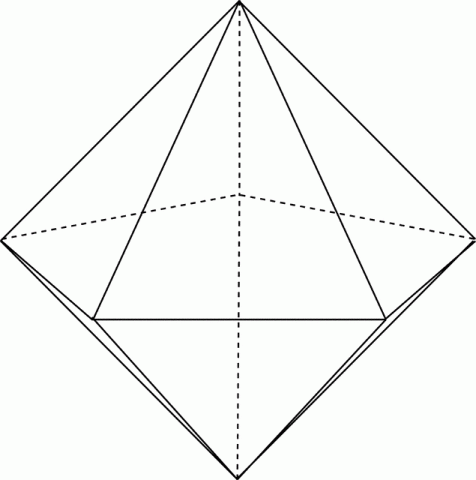
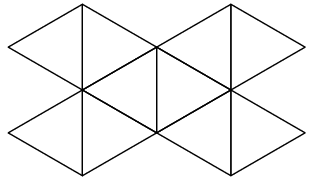
- snub disphenoid – split a tetrahedron into two wedges and join them with a band of eight triangles in the center (12 sides)
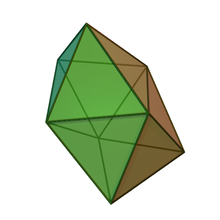
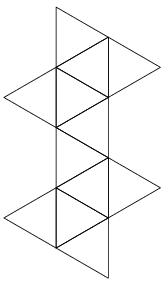
- triagumented triangular prism – attach 3 square pyramids to a triangular prism (14 sides)
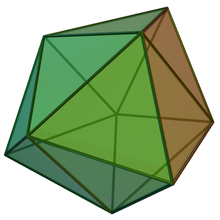
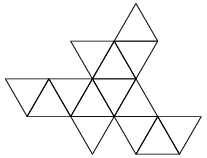
- gyroelongated square dipyramid – attach 2 square pyramids to a square antiprism (16 sides)
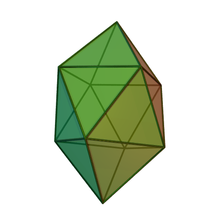

Keith Critchlow writes, “Plato discusses the doctrine that states that the essential relationships between phenomena are triangular or triadic sets and as such represent the act of the artificer of the universe when bringing ‘beautiful order’ into the four elements.”

Plato wrote, “The starting-point is, of course, universally accepted: that fire, earth, water, and air are material bodies. Now, this means that, like all bodies, they have depth, and anything with depth is necessarily surrounded by surfaces, and any rectilinear surface consists of triangles. There are two basic triangles from which all triangles are derived, and each of them has one right angle and two acute angles.” Timaeus 53c
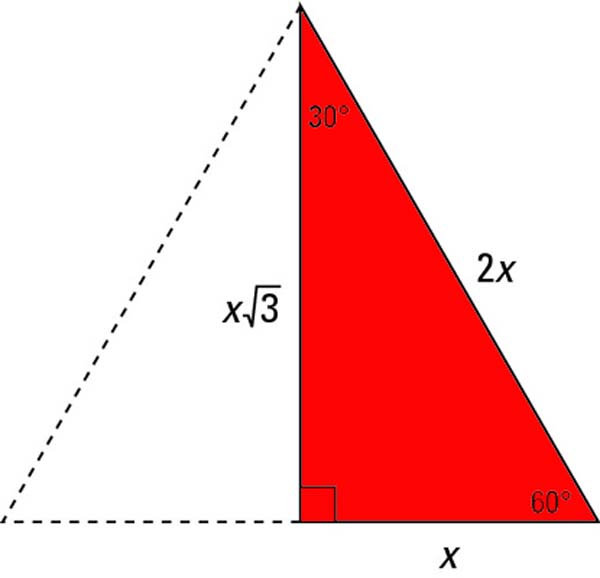
These two basic triangles are the 30º-60-90 half equilateral triangle:
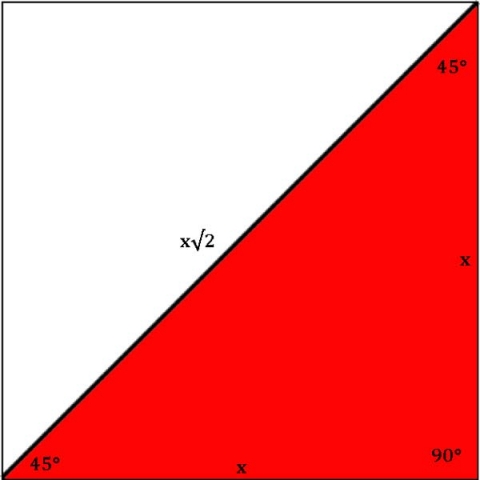
and the 45-45-90 half square:
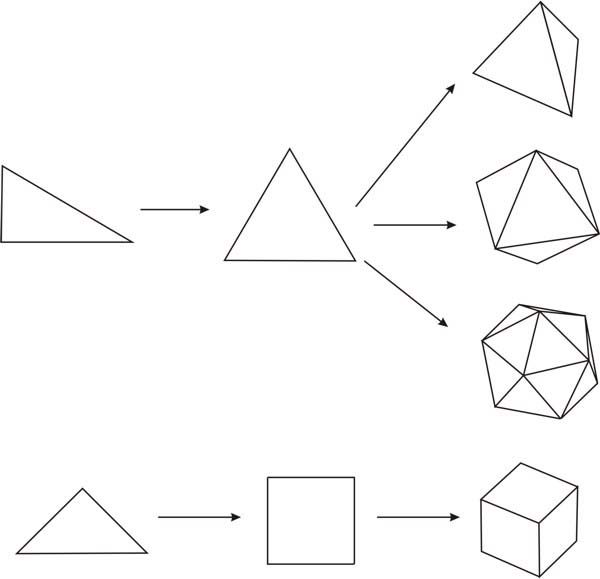
Below is an image showing the half equilateral triangle forming the equilateral triangle that then forms the tetrahedron, octahedron and icosahedron.
Below that the half square is shown forming the square then the cube.
It is true, every plane of a polygon can be reduced to a triangle. We will examine this further at the end of the article.
Think for a moment about matter on a subatomic scale as rotating spheres (toroids) moving through space. These rotating spheres are actually oscillating and moving wavelengths which create corkscrew patterns as they move through space.
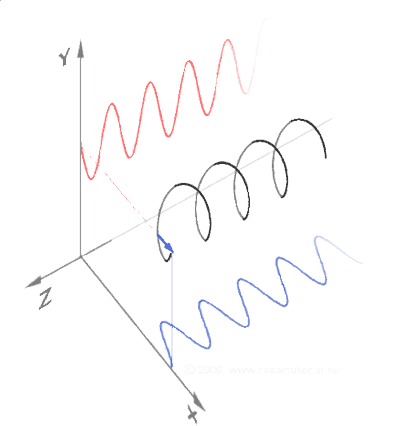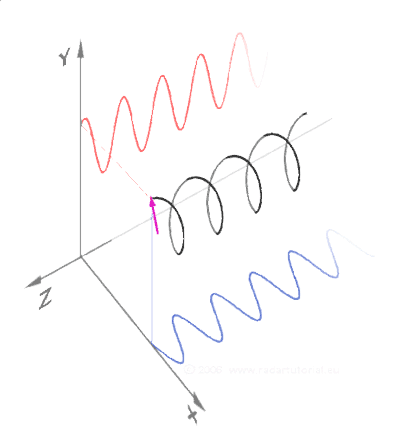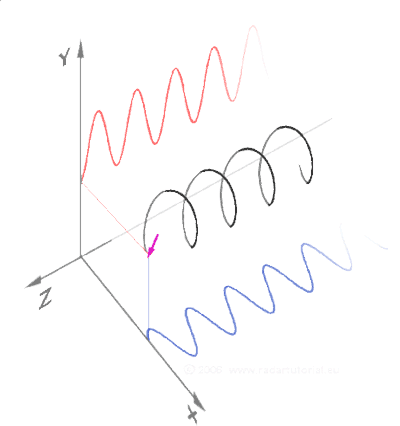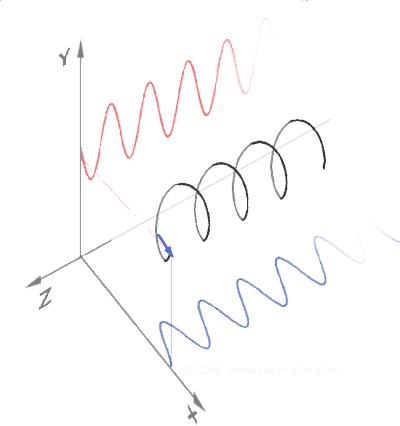
Now recall the importance of the triangle when looking at these corkscrew patterns. Right triangles are the basis of these corkscrew patterns as they move through space. Sine and cosine define the wave properties.
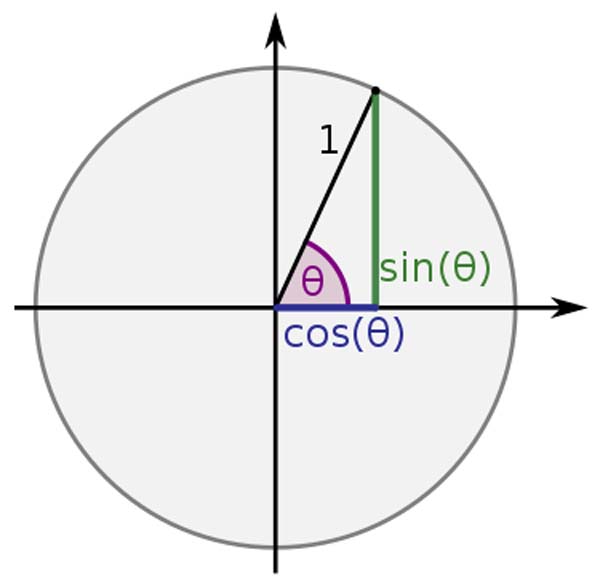
The corkscrews represent electromagnetic energy.
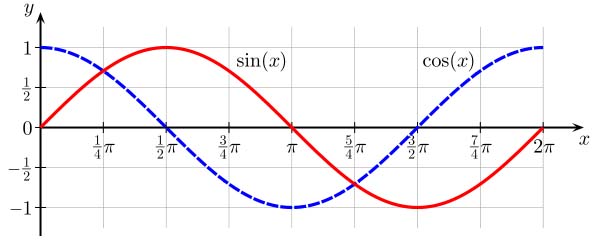
Recall that electromagnetic energy is carried on photons.
Recall that photons are tetrahedral in shape. Free photons are composed of two tetrahedra back-to-back ( triangular bipyramid on left) and confined photons are composed of two tetrahedra slid together to form a star tetrahedron or stellated octahedron (on right).
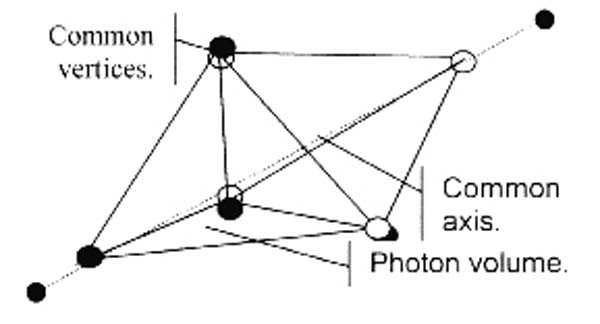

Credit: Rod Johnson (Free Photon) & Radosław Chrapkiewicz (Confined Photon)
The animation below shows a rotating star tetrahedron. You can clearly see its ‘cubic’ or crossing angle as it rotates.

Photons (or light) moves in straight line spirals (corkscrews). In the image below one color represents the electric axis, the other the magnetic axis. They spiral around each other at 90º to one another as they move through space.

Everything is boiled down to triangles representing forces or energy moving through space.

The 3D Equilateral Triangle – The Tetrahedron
Remember, the Vesica Piscis naturally generates the equilateral triangle.
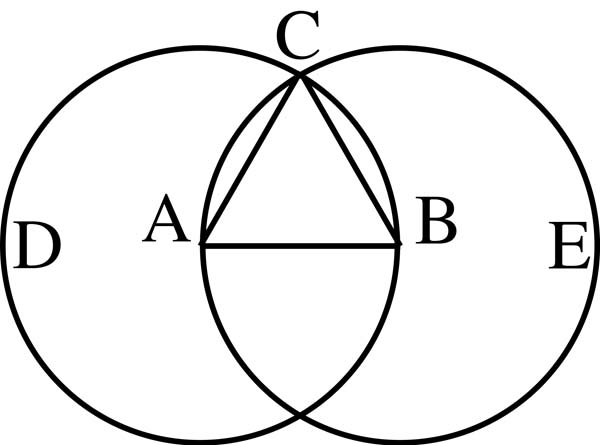
The equilateral triangle naturally generates the tetrahedron.
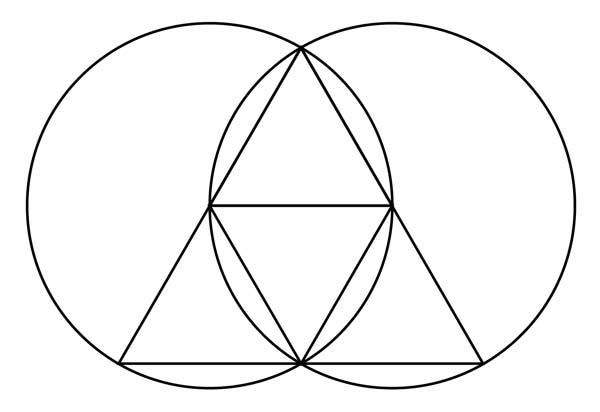
The triangle can be naturally divided into 4 smaller equilateral triangles.
These triangles fold inwards towards each other to form the tetrahedron, the first, simplest and most fundamental Platonic solid.
Below are four different representation of a tetrahedron:
- the spherical version (planar and full spherical version combined) This is one of the Neolithic stone spheres found throughout Scotland. We discuss these in Article 40.

- The full spherical version
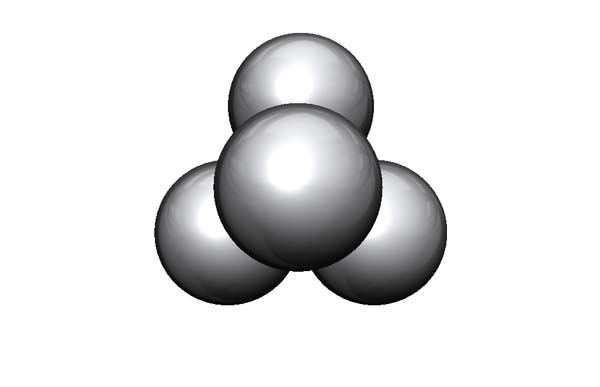
- A further spherical version made up of four spherical pebbles stacked as a tetrahedron
- The planar version with straight lines only
Brief Overview of the Platonic Solids
The Platonic Solids are the only possible convex regular polyhedra (pictured below).
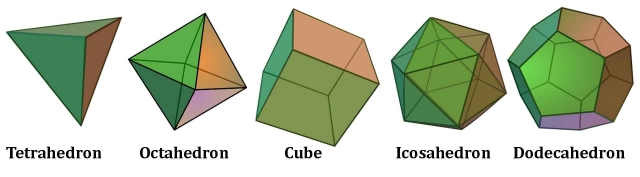
Regular polygon – 2D plane with equal sides and equal lengths (triangle, square, pentagon…etc.)
Regular polyhedron – 3D volume with equal regular polygon faces and identical vertices (5 Platonic solids)
Platonic Solids are the only shapes:
- with equal side lengths
- with equal interior angles
- that look the same from each vertex (corner point)
- with faces made of the same regular shape (triangle, square, pentagon) 3, 4, 5
- all fit perfectly in a sphere (circumsphere) with all points resting on the circumference
| Plato’s Element | Volume | Shape of Face | Faces | Edges | Corners | Sum of Angles | Dual |
| “Heaven” or Aether | Dodecahedron | pentagon | 12 | 30 | 20 | 6480 | Icosahedron |
| Fire | Tetrahedron | triangle | 4 | 6 | 4 | 720 | Tetrahedron |
| Air | Octahedron | triangle | 8 | 12 | 6 | 1440 | Cube |
| Water | Icosahedron | triangle | 20 | 30 | 12 | 3600 | Dodecahedron |
| Earth | Cube | square | 6 | 12 | 8 | 2160 | Octahedron |
Triangles and Regular Polygons
Reference Construction Lesson #28: Triangles in Polygons
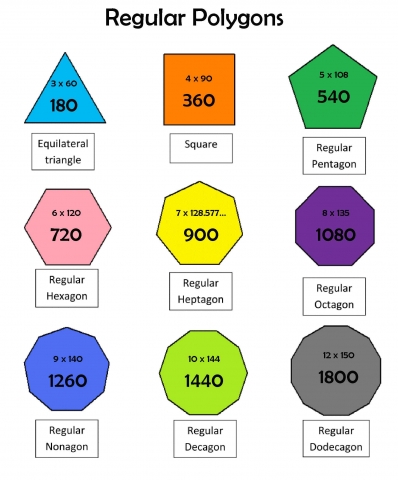
As we said above, every polygon can be reduced to a triangle. There are many ways this can be done. Also, all triangles can be subdivided into smaller triangles. Here are some examples:
Triangle – A triangle can be subdivided into smaller and smaller triangles.
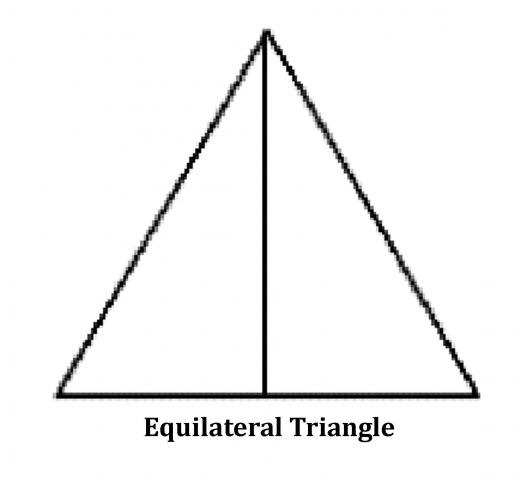
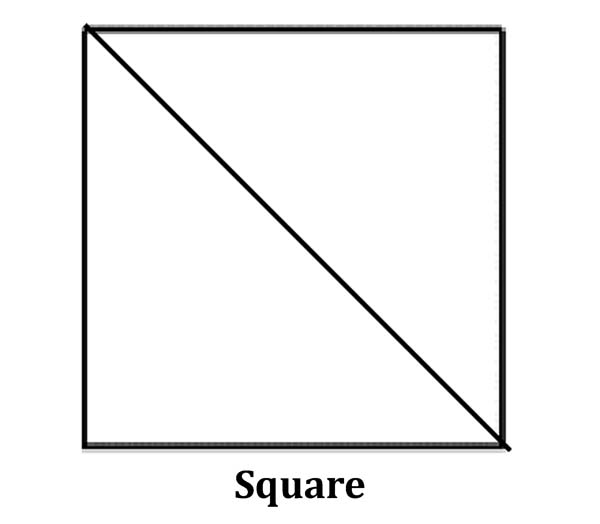
Square – A square can be divided two right triangles (90° – 45° – 45°).
Pentagon – A pentagon can be divided into 3 triangles (2 108° – 36° – 36° & 1 72° – 72° – 36° in black) or 5 triangles (54° – 54° – 72° in red).
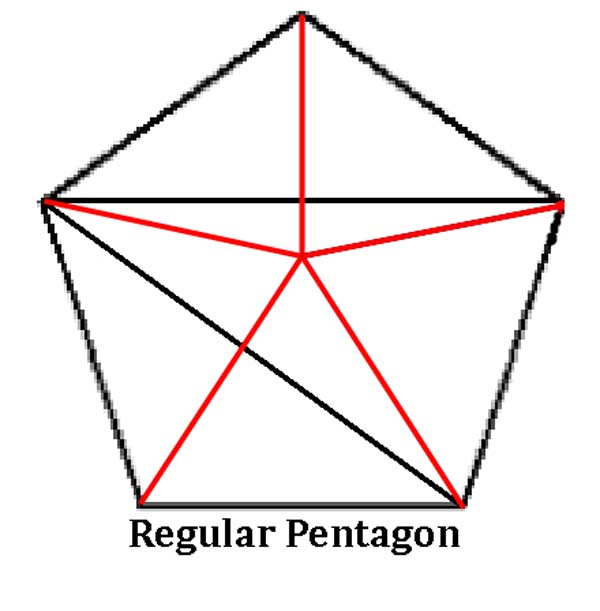
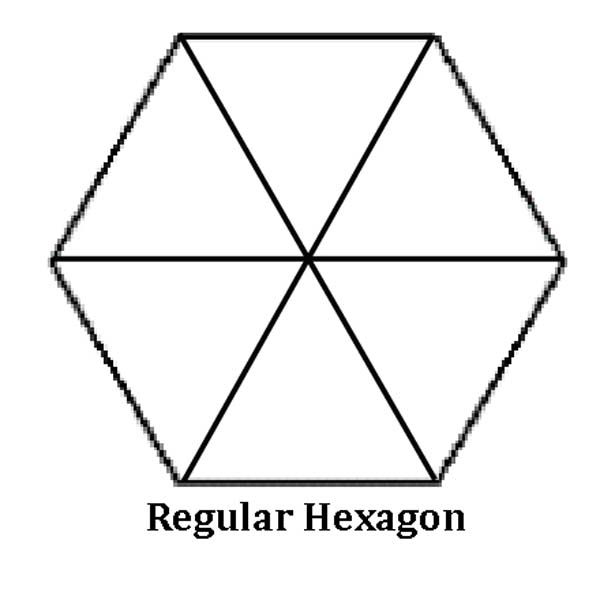
Hexagon – A hexagon can be divided into 6 equilateral triangles (60° – 60° – 60°).
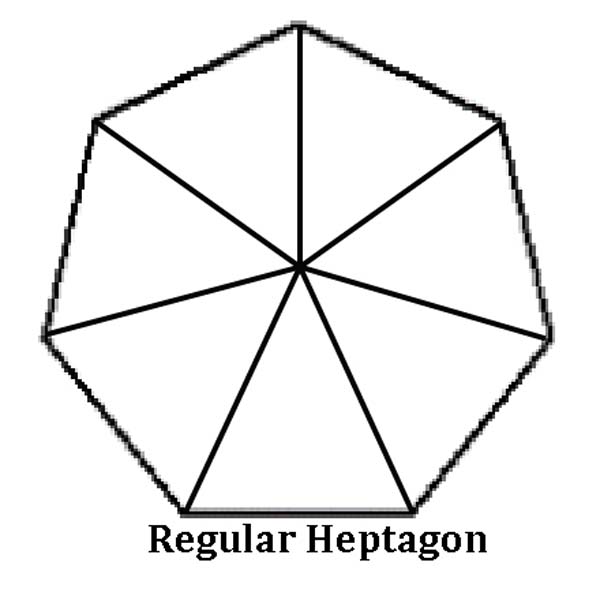
Heptagon – A heptagon can be divided into 7 triangles (64.28° – 64.28° – 51.43°).
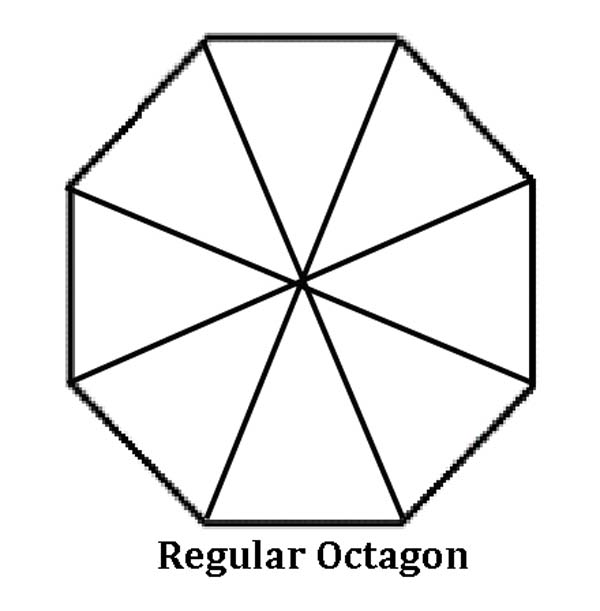
Octagon – An octagon can be divided into 8 triangles (67.5° – 67.5° – 45°).
Nonagon – A nonagon can be divided into 9 triangles (70° – 70° – 40°).
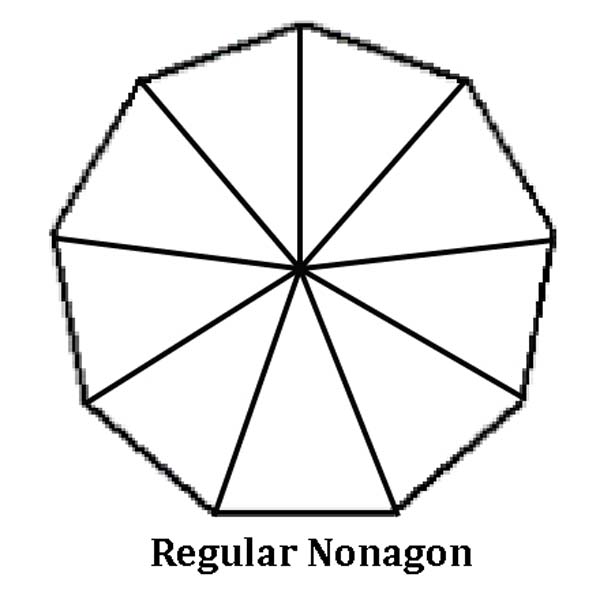
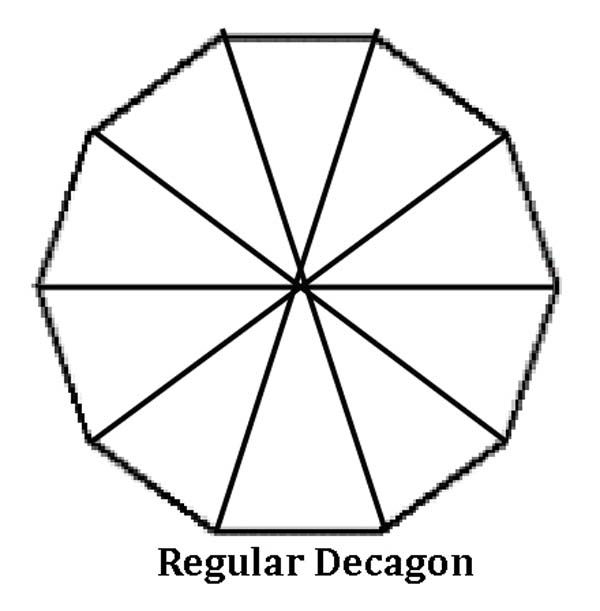
Decagon – A decagon can be divided into 10 triangles (72° – 72° – 36°).
Samuel Colman writes, “We must not consider that the circle, the triangle, and the square are simply forms, but elements representing the divine grammar of Nature. These geometric principles continue throughout the universe in orderly and exact methods, not only to secure beauty of proportion but the highest use as well.”

Triangles and the Platonic Solids
Three basic triangles are required to fabricate these five solids:
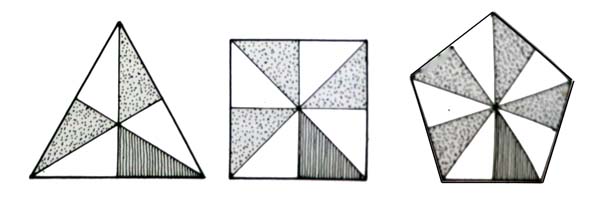
Credit: Keith Critchlow, Time Stands Still
- The scalene half-equilateral triangle: 90º-60º-30º
- Makes the tetrahedron, octahedron, and icosahedron.
- The isosceles half square: 90º-45º-45º
- Makes the cube.
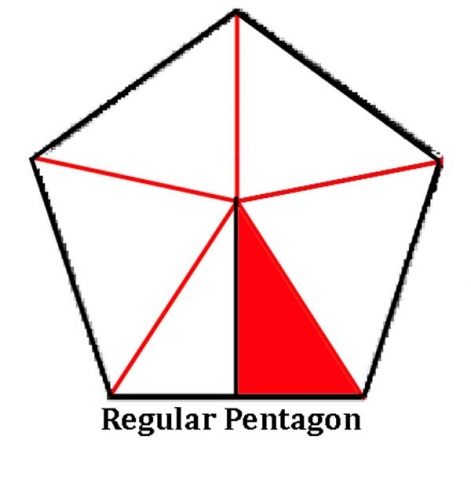
- The scalene one-tenth of a regular pentagon: 90º-54º-36º (in red below)
- Makes the dodecahedron.
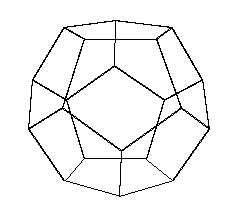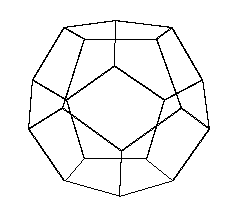
Platonic Solid Nets
A ‘Geometry Net’ is a flattened out three dimensional solid. When you cut out the net, fold it and glue it together you will create the 3D shape.
In the next section of articles on the Platonic Solids we will look at the nets of each solid in detail. Here is a brief look:
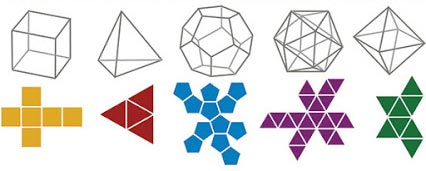
In this article we will look specifically at the nets formed solely from the three triangles listed above.

Credit: Keith Critchlow, Time Stands Still
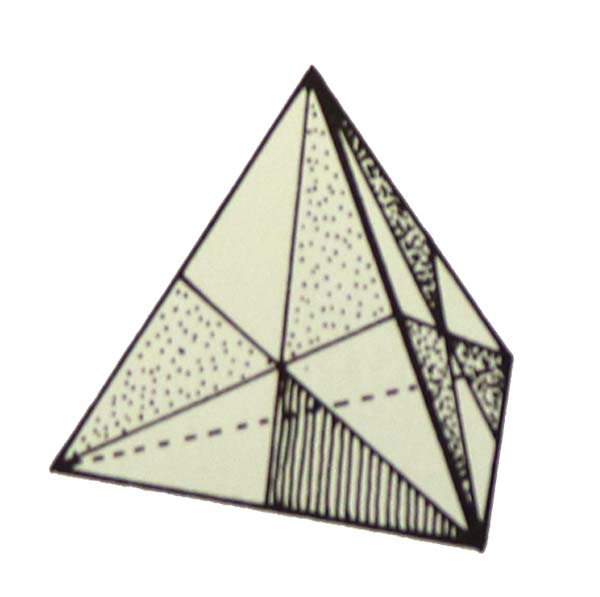
Tetrahedron
The tetrahedron is composed of:
24 30-60-90 triangles or
8 30-60-90 larger triangles.
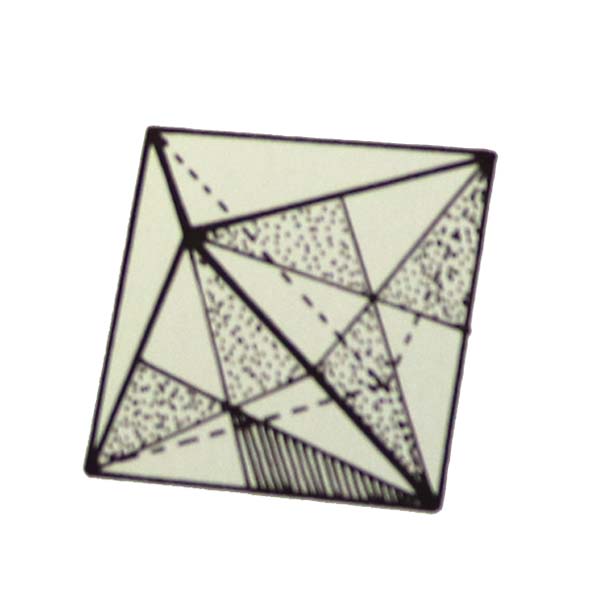
Octahedron
The octahedron is composed of 48 30-60-90 triangles.
Icosahedron
The icosahedron is composed of 120 30-60-90 triangles.

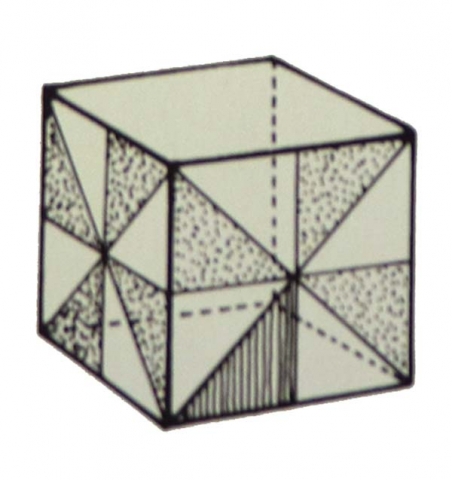
Cube
The cube is composed of 12, 24 or 48 90-45-45 triangles.
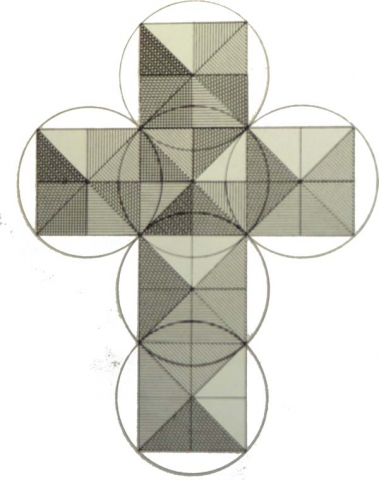
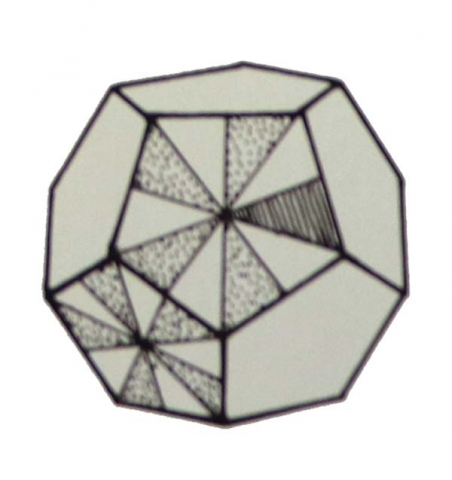
Dodecahedron
The dodecahedron is composed of 60 pairs of 90-54-36 or 120 triangles total.

- Edmondson, Amy, A Fuller Explanation: The Synergetic Geometry of R. Buckminster Fuller, Burkhauser Boston, 1987
- ibid.
Recent Comments