In this article we will expand on a very important aspect of the Tetrad and squares – the square root 2 ratio. We will also briefly discuss the Silver Ratio.

We discussed the square root of 2 in Articles 24-26.
The Square Root of 2: √2
√2 represents the Diagonal of a Square.
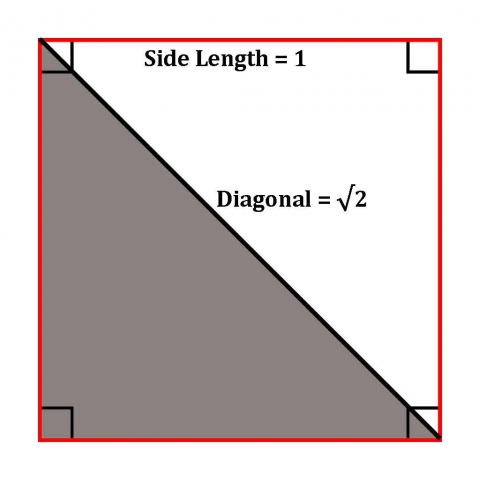
Herein lies an important difference between arithmetic and geometry. As Keith Critchlow writes, “The diagonal of a square with sides cannot be expressed in whole numbers but can be drawn with great precision geometrically. The square root of two never reaches a final whole number solution. Plato called it arretos, meaning ineffable.”
In the symmetry of the square lies the power of self-reproduction and a potentially infinite multiplicity symbolized by the √2 and expressed geometrically below. This self-reproductive power inherently expands to infinity, producing as it grows, all the whole numbers.
The side of a square is called its root (√).
If the length of the side of a square is 1 then the diagonal of the square is √2. 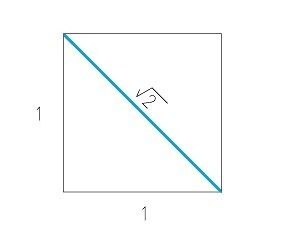
Using the simple Pythagorean theorem: a2 + b2 = c2, we easily see how the diagonal equals √2.
a = 1
b = 1
c = the hypotenuse (diagonal).
So, 12 +12 = c2.
12 = 1 so this makes it:
1 + 1 = c2.
2 = c2.
Therefore, √2 = c.
Numerically √2 = 1.4142135…
It is an ‘irrational’ or ‘supra-rational’ number, meaning the decimals will go on to infinity, never repeating.
Bruce Rawles writes, “The √2 embodies a profound principle of the whole being more than the sum of its parts.
The orthogonal dimensions (axes at right angles) form the conjugal union of the horizontal and vertical which give birth to the greater offspring of the hypotenuse.
The new generation possesses the capacity for synthesis, growth, integration and reconciliation of polarities by spanning both perspectives equally.
The root of two originating from the square leads to a greater unity, a higher expression of its essential truth, faithful to its lineage.
The fact that the root is irrational expresses the concept that our higher dimensional faculties can’t always necessarily be expressed in lower order dimensional terms.”1
Thus, as Robert Lawlor writes, “The extreme, essential polarity of the universe, Unity and Multiplicity, is perfectly represented and observable in the simple drawing of the square and its diagonal.”2

The Silver Ratio
The Silver Ratio = 1 + √2.
The Silver ratio is any two quantities in which:
The sum of the smaller and twice the larger of the quantities is to the larger quantity as the larger is to the smaller.
(smaller + 2 * larger) : larger :: larger : smaller
This ratio, like the golden ratio and square roots of 2, 3, and 5 is an irrational or supra-rational number.
It is: 2.4142135623730950488… or as we said 1 + √2.
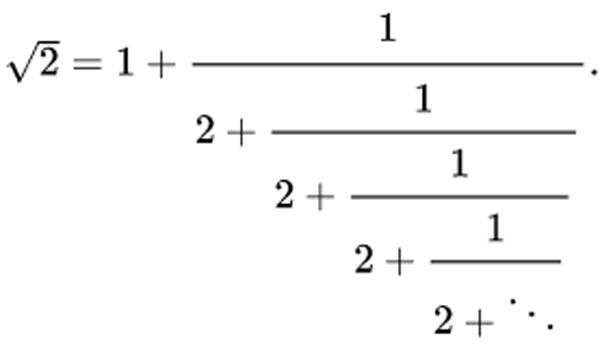
Like the Golden Ratio and Square Roots, the Silver Ratio can be expressed as a continued fraction:
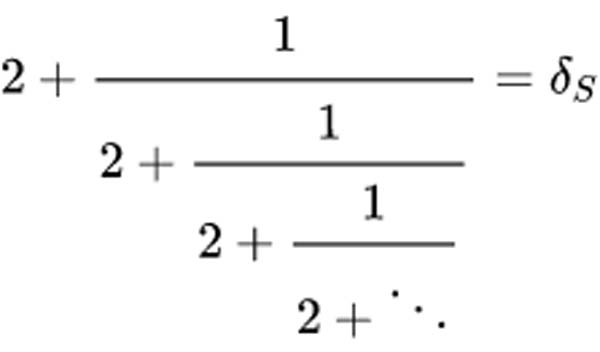
Like the Fibonacci sequence converges on the Golden Ratio, the Pell sequence converges on the Silver Ratio.
Pell numbers are an infinite sequence of integers that comprise the denominators of the closest rational approximations to the √2.
This sequence begins: 1/1; 3/2; 7/5; 17/12; 41/29…etc.
The Pell number sequence is therefore: 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860…
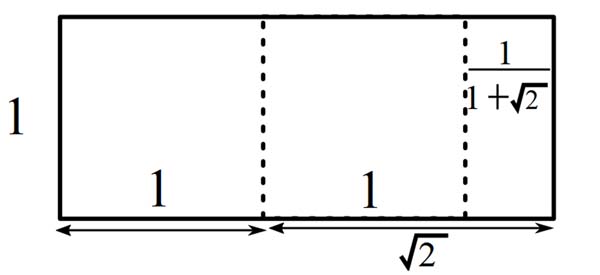
The Silver Rectangle
In the silver rectangle, the sides are in a 1 to 1 + √2 ratio.
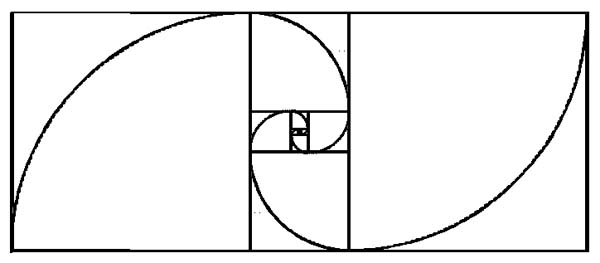
The Silver Spiral
The sides of the squares used to construct a silver spiral are all Pell numbers.
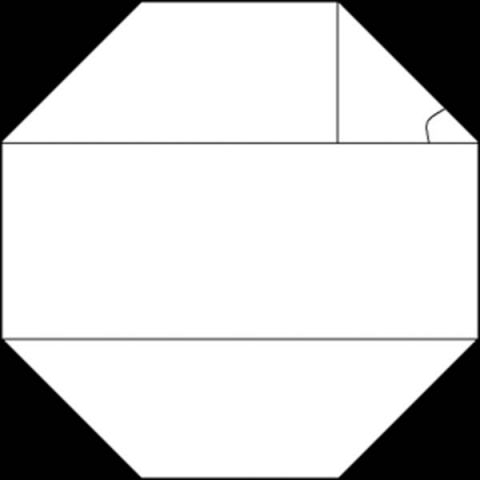
The Silver Ratio & The Octagon
The silver ratio is found in the octagon as seen here.
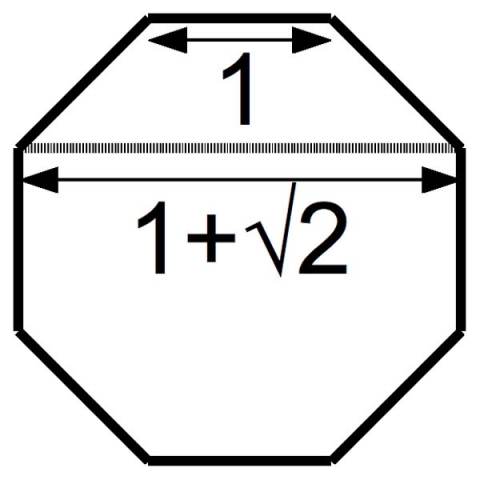
This means the central portion of the octagon is a silver rectangle.
√2 and the Human Body
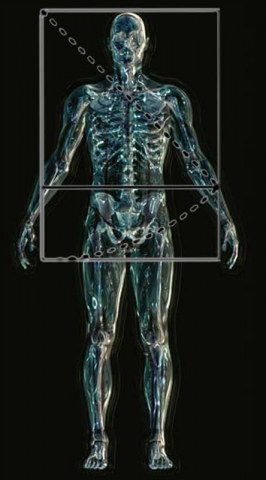
The height of the human body is divided into the harmonic division of √2. Here a root 2 rectanlge marks the top of the head, navel and groin.
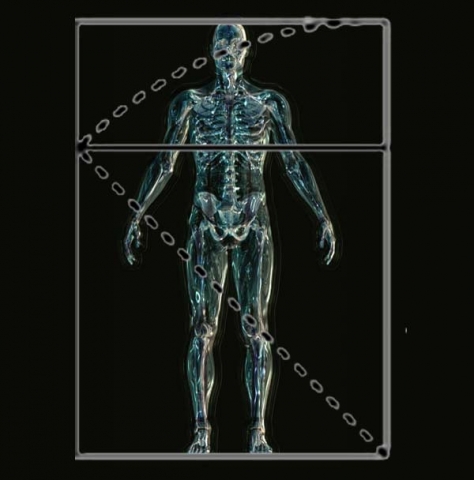
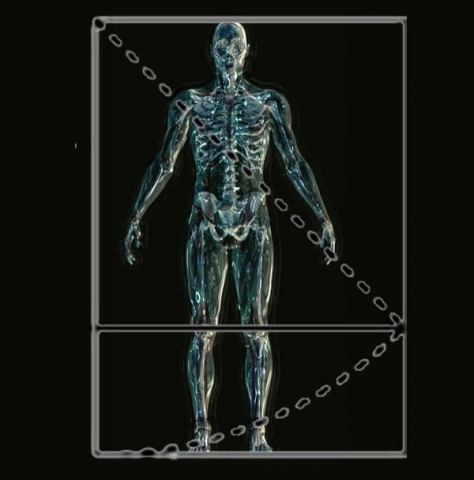
When a √2 rectangle is drawn around the entire body, root 2 marks the vital solar plexus area and the level of the knees.
The body will measure (2 – √2) from the soles of the feet to the navel center
and (√2 – 1) from the navel center to the top of the head.
The √2 and Design – Paper
Interestingly, there is a connection between paper size, the square root of 2, the Earth and Moon. This work is courtesy of Michael Schneider found here: Michael S. Schneider – Constructing the Universe
International Standard paper Size employs the continuous geometric proportion of 2:√2::√2:1. The Silver Ratio is also found in paper sizes.
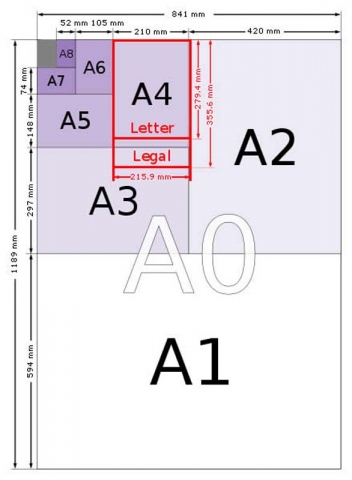
Removing a square from a sheet of such paper leaves a rectangle with silver ratio proportions (1:√2-1) or (1+√2:1).
Folding a √2 rectangle in half gives you two smaller √2 rectangles.
Folding a sheet of A3 (2√2) in half gives you two sheets of A4 (each √2:1).
These proportions are also related to the Squaring of the Circle.
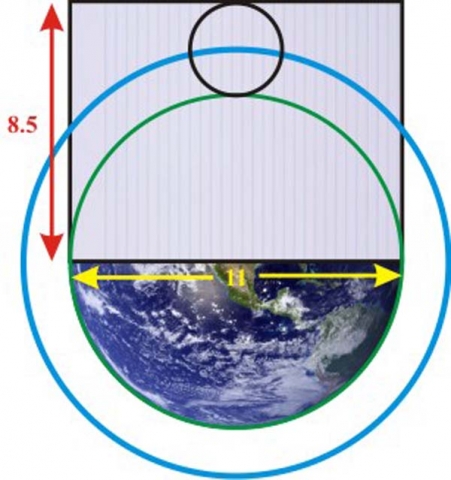
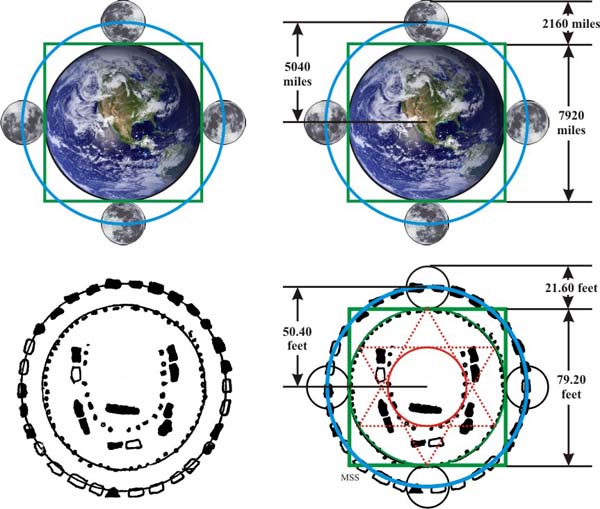
The polar diameter of the Earth is 7920 miles. The Moon’s diameter is 2160 miles.
The Earth’s diameter to the Moon’s diameter = 11/3.

“Since the Earth isn’t a perfect sphere but nearly an oblate spheroid, it’s not appropriate to apply perfect pi (3.14159…) to it. Instead, we’ll use the well-known traditional approximation of pi as 22/7 (or 3.14285…), which is distorted by less than two feet in a mile. When the Earth and Moon’s dimensions are considered with this value of pi, a curious mathematical situation occurs: a squared-circle.”3
See the image below.
The green square has a diameter of 7920 miles. Its perimeter = 7920 * 4 = 31,680.
The moon, brought down to the Earth’s surface, creates the blue circle. The blue circle intersects the center of the moon. The center of the blue circle is the center of the Earth.
The circumference of the blue circle is 2πr = 2 * 22/7 * (3960 + 1080) = 31,680.

The perimeter of the square equals the circumference of the circle. The Earth and Moon ‘square the circle’.
Not only does the √2 show up in International paper sizes, but also in U.S. paper sizes.
“We find that the distance from the center of the Earth to the top of the Moon is to the Earth’s diameter as 8.5 is to 11. This is the ratio of sides of ordinary U.S. writing paper known as ‘Letter’ size. This is the paper size familiar to most Americans, found commonly in our printers.”4
Letter size can also be seen in this way:
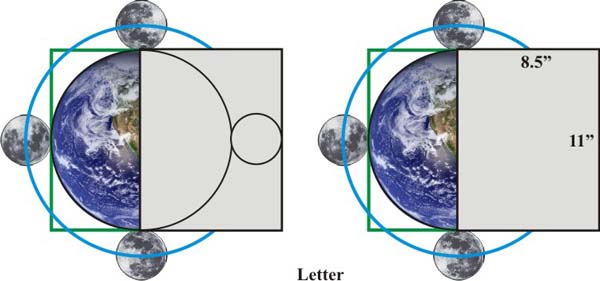
Credit: Michael Schneider
Legal size paper can be seen in this way:
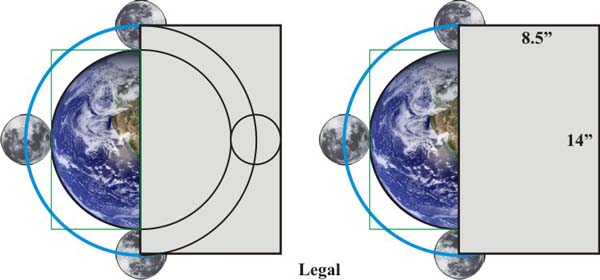
Credit: Michael Schneider
“Most astonishingly, the plan of Stonehenge resembles this Earth-Moon scheme in miniature. Its two concentric outer rings of stones relate by a “squared circle,” and its measures reveal the same numbers but in feet instead of miles.”5
Credit: Michael Schneider
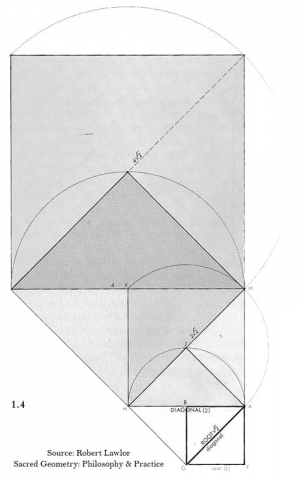
The square and its diagonal express the creation of Two from Unity (the initial square) and a consequent proliferation of number through a geometric sequence.
Reference Construction Lesson #12: Square Root 2
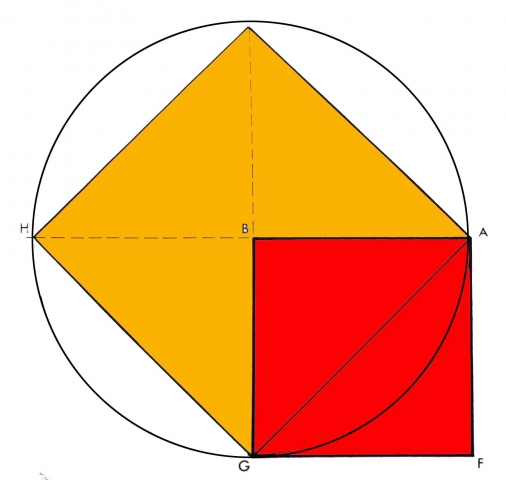
The side of square 1 is 1. Its area is 1 because 1 x 1 = 1
The side of square 1, called its ‘root’ is √1, and that of square 2 is √2.
The simple act of drawing the diagonal has given rise to 2, not because the square has been divided in half, but because square 2 is implied.
The diagonal of square 1 is the √2.
The diagonal of square 1 equals the side of square 2.
The diagonal of square 2 is equal to 2, exactly twice the side of the primary square.
Hence, Square 2 is exactly double in area to square 1.
As the squares increase in size, their root-diagonal relationships remain proportional identities.
Two paradoxes are revealed in the act of its division by the diagonal:
1st Paradox: the coinciding of the two functions of root and diagonal in the geometric moment of the √2. That is, the same line is both root and diagonal. This illustrates the paradox of sameness and difference. One can be the same and different simultaneously.
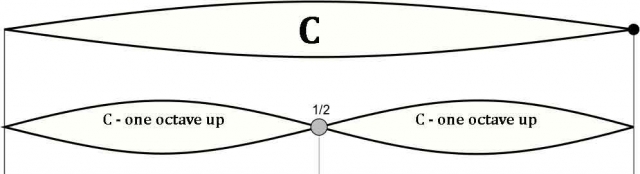
2nd Paradox: the fact that the half (the square halved by the diagonal) produces the double, as in the generation of musical tone and in the mystery of biological growth from cellular division.
This is the law of the octave. That is, halving = doubling. In this case, halving the square through its diagonal equals a square twice its size. Two grows out of the division of One.
Geometric Progressions
Reference Construction Lesson #34: Square Root – Outward Progression

“This type of progression is called a ‘geometric progression’ where the numerator, when multiplied by the denominator of the second relationship is equal to the multiplication of the numerator of the second relationship by the denominator of the first relationship.”5
This is also known as the law of cross multiplication.

This holds true for any ratios in the progression whether in sequence or not.
“The square divided by its diagonal provides an archetypal model for geometric proportions and progressions of this type, that is 1 : √2 :: √2 : 2, where each term (or ratio) is multiplied by a constant value in order to achieve the next term in the progression. A fixed, proportional increase or rate can be the generative pattern for other infinitely expanding geometric progressions.”6
This process represents the alchemical axiom of creation.
All is formed by two elements:
- Proportion – fixed, immutable component
- Progression – volatile, mutable component
This shows how the creation of 2 leads to endless proliferation through the geometric progression a:b::b:c, etc., or expressed numerically:
1:2 :: 2:4 :: 4:8 :: 16:32 :: 32:64…
No matter how vast the numerical relationships become, this proportion a:b::b:c remains unchanged.
“The √2 thus represents the power of multiplicity which can extend itself both towards unlimited expansion and towards utterly minute finiteness.”7
“The relationship between the fixed and the volatile (between proportion and progression) is a key to Sacred Geometry: everything which is manifest, be it in the physical world or in the world of mental images and conceptions, belongs to the ever-flowing progressions of constant change; it is only the non-manifest realm of Principles which is immutable.”8

Reference Construction Lesson #35: Square Root 2 – Inward Progression
This drawing is a variation of the previous geometric progression, but extended in the opposite direction of diminution.
The square and its diagonal express the creation of Two from Unity (the original square).
They also express the consequent proliferation of number through a geometric sequence.
Remember, “The square root of two is the geometric function which represents the universal metaphor of the root, and the root represents the principle of transformation. This moment of transformation is everywhere before us, in the roots of plants transforming mineral into vegetal, in the leaves transforming sunlight into live supporting tissue, in rock and stone being weathered and worn down into molecular gases and liquid, liquid into gas, gas into solid, light into heat, heat into mechanical movement; in the germination of a seed…This transformation goes on in every passing moment as well as in the long aeons of evolutionary cycles. Transformation is the ubiquitous condition of the worlds, and their evolution from mineral to plant to animal, kingdom emerging out of kingdom, volume forming itself out of the converging vector extensions of a preceding volume. There is periodicity, rhythm, oscillation, pattern, frequency, all measurable in time and space units.”9

Review Articles 24-25 for more square root 2 symbolism.
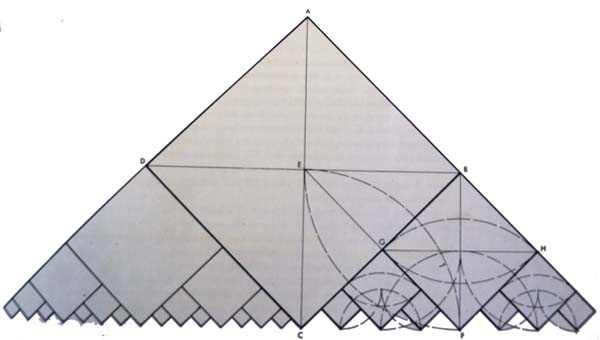
Reference Construction Lesson #36: Root 2 Expansion
In this drawing the incremental growth increases by root2 with each iteration.
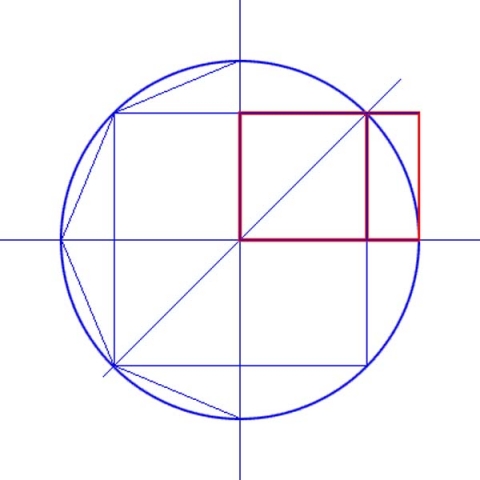
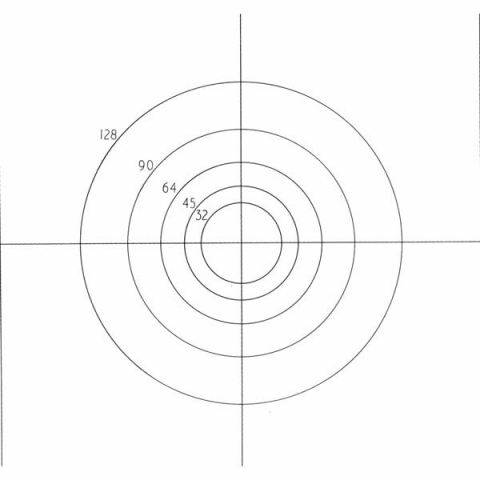
This proportion is related to impact craters. The crust gets liquefies by the impact of the meteor. This creates expanding rings. As they move outwards they cool down, solidify and lock in the relationship. This relationship is the square root of 2. It can be seen in impact craters on the Earth, Moon and Mars.
Below is an image of one such crater: Orientale Crater on the Moon.

- Rawles, Bruce, Sacred Geometry Tutorial, The Geometry Code, https://www.geometrycode.com/sacred-geometry/
- Lawlor, Robert, Sacred Geometry: Philosophy & Practice, Thames & Hudson, 1982
- Schneider, Michael, What do US paper sizes have in common with the Earth and Moon?, 2012, http://www.constructingtheuniverse.com/US%20Paper%20Earth%20Moon.html
- ibid.
- Lawlor, Robert, Sacred Geometry: Philosophy & Practice, Thames & Hudson, 1982
- ibid.
- ibid.
- ibid.
- ibid.
Recent Comments