We will now move into a discussion of the cube and its associated Archimedean and Catalan solids. However, we will only briefly mention the cuboctahedron, saving it for the Article 49 where we will go into this particular shape in far greater detail.
Here we see the most familiar of all Platonic solids, the cube.

The Cube – 2160º
The cube is also called the Hexahedron, meaning “Six Faces”.
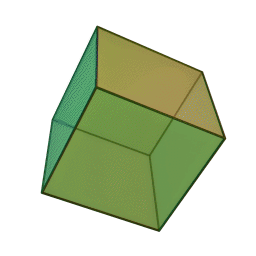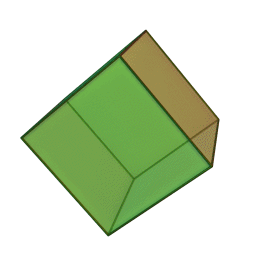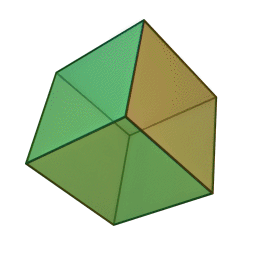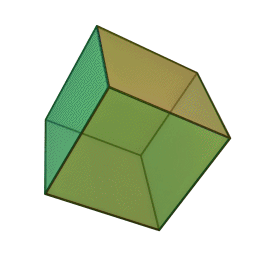
It has:
- 6 faces
- 8 corners
- 12 edges

It has 90 degree interior angles with three faces meeting at each vertex.
It is related to the element ‘Earth’ by Plato due to the stability of its square bases. He wrote, “Let’s begin by assigning the cube to earth, because, of the for bodies, earth is the most inert – the hardest to move and the readiest to hold its shape – and this description must above fit the figure with the most secure faces.” Timaeus 55e

Recall that the square is associated with Earth, solid ground, matter and mass. The cube is the square taken to a ‘higher power’.
The 6 faces correspond to the 6 directions: North, South, East, West, Zenith, Nadir.

6 is the first perfect number. This means the factors sum to itself.
1 + 2 + 3 = 6
The cube has:
- 12 edges
- 12 face diagonals (√2)
- 4 interior diagonals (√3)

This equals 28 straight paths joining the cube’s 8 vertices to each other.
28 is the 2nd perfect number.
1 + 2 + 4 + 7 + 14 = 28
There are 28 phases in each moon cycle.

The Dual of the Cube is the Octahedron.


If the cube has side lengths of 1, then its dual the octahedron will have edge lengths of √2. This is because the octahedron’s edges are the diagonals of the cubes faces.

Recall, that the diagonal of a square with side lengths of 1 is √2.

The Sum of the angles of the Cube is 2160°
(90 x 4) = 360; 360 x 6 = 2160.
2160 hertz = C# in music.

The Projections of the Cube are as follows:

Note the hexagonal view. This gives a clue to the intimate relationship between the cube and hexagon.
The hexagon also shows up as a cross-section of the cube when the cube is intersected by a plane perpendicular to its diagonal and is cut in half.

Here are the cross sections of the cube when cut at the origin within various planes.

Cubic, Hexad, and Octad Geometry is known for its role in structure, function and order.
It is seen throughout the natural world in holding and making membranes, or creating barriers. This is very commonly seen in the structure of cells in plants, animals and humans.

In the mineral world, sodium chloride (NaCl) or common table salt naturally forms cubic crystals.

Fluorite and Pyrite crystals are also often cubic in structure.


The Net of the Cube is seen below:

It is interesting to note that there are 11 distinct nets for the cube. This is the same number of nets for the octahedron. The cube nets are seen below:

A cube has an inradius, midradius and circumradius as follows:
Inradius = ½
Midradius = ½ √2
Circumradius = ½ √3
Here is the cube with its insphere:

Here is the cube with its circumsphere:

Eight Spheres Make a Cube:

Note these are not closely-packed spheres. They are stacked spheres.
In Close-packing, 14 Spheres make a Cube:
It begins with 6 close-packed spheres that create an octahedron.

A second set of 8 spheres is then introduced into the interstices.


The cube emerges as the dual of the octahedron.
The Cube in Metatron’s Cube:

The Spherical Cube looks as follows:

The Stereographic Projection of the Cube is as follows:

The Cube Tessellates:

The cube is the only Platonic solid that tessellates.

Other polyhedra that tessellate include:
- triangular prism
- hexagonal prism
- truncated octahedron (Archimedean solid)
- rhombic dodecahedron (Catalan solid)
- elongated dodecahedron
Volume = s3 s = side length
“As the volume of a cube is the third power of its sides s * s * s, third powers are called cubes, by analogy with squares and second powers.”1

Remember, the diagonal of a cube is √3 if the side lengths are 1.
If side lengths are 1 then:
The longer diagonal is √3.

The shorter diagonal is √2.

Surface Area = 6s2 s = side length
Recall the significance of the number 2160.
2160 = Sum of the Cube’s Angles
2160 = the diameter of the Moon in miles
2160 years in each age of the Zodiac (1 Great Month or Zodiacal Age) in the 25,920 Great Year (Precession of the Equinoxes)
2160 (related to 432)
- 432/2 = 216
- 2160/2 = 1080 = octagon
- 2160/3 = 720 = hexagon
- 2160/4 = 540 = pentagon
- 2160/5 = 432
- 2160/6 = 360 = square and circle
- 2160 = diameter of the Moon (half 4320)
- The diameter of the Sun (twice 432000) = 864,000
- 864,000 seconds in a day or
- 432,000 seconds of light (day)
- 432,000 seconds of darkness (night)
- 4322 = 186,624 miles/second (speed of light)
- 432 the only whole number when squared comes into .01% accuracy measuring the speed of light.
- The accepted value for the speed of light = 186,282 miles/second (.01% difference).

The Cube in Religious Traditions
- Islam’s annual pilgrimage is to the Kaaba (“The Cube”) in Mecca, Saudi Arabia. This is the most sacred site in Islam.

- The Sanctuary of the Temple of Solomon was a 30 foot cube. This is the most sacred space in Judaic tradition – the Sanctum Sanctorum, Holy of Holies, in Solomon’s Temple.


- The Holy City of New Jerusalem in Revelations is a cube. It is 12,000 furlongs cubed. New Jerusalem represents the most holy space or place in Christianity.

- The ‘perfect ashlar’ in Masonry is a cube.
- “Masonry adopts the ashlar as a symbol in two forms: in its rude, unhewn state, in which it is called the rough ashlar – referring to the uncultivated, ignorant condition of mankind, yet a mere mass of material blindness and moral confusion; and also as the perfect ashlar, where the mind has assumed its harmonic proportions and symbolic form.”2

“We are all works in progress.”
The Cube also shows up in Science and Nature.
In Dr. Harold Aspden’s Aether Physics Model, the Aether has a liquid crystal structure. Fluid crystals are standing waves of geometry.

Dr. Aspden’s Aether Units are called Quons. They consist of a cube of Aether space with two rotating spheres (muons) inside each cube. The muons are stacked one on top of the other and they rotate in opposite directions.

This forms a double torus flow structure.

Dr. Aspden also promotes the fractal-holographic structure of the Universe. There are cubes within cubes in his model.

There are also large-scale structures in space on the solar level that are structured as cubes.
Space domains are the cellular structure on the solar scale. They are approximately 500 light years in diameter. There is a space domain for each star. The star/sun sits at the center of each cube.

In Walter Russell’s Physics Model, the cube-sphere is the Aether Unit. It consists of a pulsing cube-sphere. The cube is the sphere expanding outwards. The sphere is the compressed form.


Credit: Walter Russell
In The Seth Material the Aether is composed of an invisible, infinite, structure of cubes within cubes. They cannot be seen but they are constantly trembling and mobile.

In the work of Max Planck, there is a cubic structure of ‘space’ or Aether.

Two tetrahedra (star tetrahedron) fill exactly 2/3 (6.66) of a cube out of a volume of 10.

Planck’s constant is 6.626, which is very close to 6.66. The difference in numbers relates to Coulombs resistance.
Incidentally, the gravitational constant is also close to 6.66. It is 6.674. It also has a tetrahedral relationship.
In the work of Dr. Robert Moon the oxygen molecule has a cubic structure. There are 8 corners of a cube and 8 protons in oxygen.

The cube shows up frequently in the structure of molecules. There are cubic structures to many molecules and there are many square (90º) bonding patterns.

Cubic structures also show up in the shape of soil aggregates or PEDS.

They are also a common structure of crystals. There are six crystal family systems and they are all derived from the cube.

Furthermore, plant cells are often cubical in shape. They can also be rectangular or hexagonal.

All these topics are covered in great detail throughout the Science section of Cosmic Core.
Cubing the Sphere
Recall from Article 38 that the circle (or sphere) represents pure, unmanifest spirit-space; the “Heavens”, or “Time/Space”.
The square (or cube) represents the manifest and comprehensible world; the Earth, or “Space/Time”.

Credit: Michael Schneider
Squaring the Circle or ‘Cubing the Sphere’ is meant to mean the establishment of heaven on Earth. This entails the spiritual transformation of individuals which results in the spiritual transformation of the Earth as a whole. The transformation comes from within.
This ‘establishment of heaven on Earth’ refers to the New Jerusalem of Christianity, the Star of David of Judaism, and temple construction in Masonry.

Scott Onstott teaches that the Cube Volume equaling the Sphere volume is related to the golden ratio.3
The length of the side of the cube has the ratio of phi (1.618) to the radius of the sphere.
Or: side length of cube = 1 and radius of sphere = 1/phi.

Credit: Scott Onstott
Volume of a cube = s3
Volume of a sphere = .333333…x πr3 + πr3
Here Onstott has rewritten the formula for the volume of a sphere to emphasize the important pattern of repeating threes. This suggests a tetrahedron in a cube.
The Cube and the Tetrahedron
A tetrahedron nests within the cube.
If you draw a single diagonal line on every face of a cube so they join at the corners, you will have defined the edges of a tetrahedron.

The volume of the tetrahedron is 1/3 that of the cube.
The tetrahedron side length = √2 * cube edge length.
Recall that the diagonal of a square is √2 if the side length is 1. You can see from the above image that the side of the tetrahedron is the diagonal of the square. Hence, the side length of the tetrahedron will be √2 multiplied by the side length of the cube.
Here are two interlocking tetrahedra (star tetrahedron or stellated octahedra) in a cube:

Note the ‘cubic angle’ and ‘cross’ of the star tetrahedron.


Simply by using the diagonal of the cube we are able to form the star-tetrahedron or interlocking tetrahedra.
As you can see, if we connect the tips of the star tetrahedron together we will get a cube.
The Cube and the Octahedron
The Cube and Octahedron are Duals. Connecting the centers of faces creates the dual solid.

The octahedron’s points are truncated to form the cube, and vice versa.

The Cube and the Dodecahedron
A cube fits within a dodecahedron.
A cube has 12 edges. The cube will have one edge along each of the twelve faces of the dodecahedron, on which the edge of the cube is a diagonal of a pentagon face of the dodecahedron. (The diagonal of a pentagon would be one of the five lines forming the pentagram of the pentagon.)
Each of the colored lines below represents a different cube found in the dodecahedron. There are 5 total: red, yellow, green, blue, and black.

The compound of five cubes that forms a dodecahedron is discussed below.
dodecahedron side = 1
cube side length = phi
You can also see how one can build a dodecahedron by adding 6 ‘roof’ shapes to the 6 faces of a cube.
An outward expansion is required, where each face of the cube sprouts a slanting “rooftop” made of five equidistant lines in order to turn into the dodecahedron.


The Chamfered Cube and the Dodecahedron
Chamfering a cube is the same as cantellation. The edges are truncated instead of the corners being truncated.
The cube transforms into the dodecahedron if the edges of the cube are pushed into planes.

Credit: Frank Chester
A Dodecahedron folds inside out to form a Cube
Furthermore, a cube can turn inside out to form a dodecahedron…and vice versa.





See here for an animated visualization: https://www.youtube.com/watch?v=PyXyOOR63Ms
Compound of Three Cubes
The compound of three cubes is a symmetric arrangement of 3 cubes. It can be constructed by superimposing three identical cubes, and then rotating each by 45 degrees about a separate axis. It is also a stellation of the rhombicuboctahedron.

It has:
- 6 + 12 Square Faces
- 36 Edges
- 24 Vertices
Compound of Five Cubes
The compound of five cubes is composed of 5 cubes, as its name suggests. It is dual to the compound of five octahedra.
It can also be seen as a faceting of a regular dodecahedron.
Each of the 5 cubes can be seen below in a different color.

It has:
- 30 square faces
- 60 edges
- 20 vertices
This shape can also be made from the compound of ten tetrahedra (pictured below) by replacing each star tetrahedron with a cube.

A second five-cube compound also exists. This one has octahedral symmetry. It is generated by adding a fifth cube to the standard 4-cube compound. Seen below are the 4-cube compound (Bakos compound) on the left and the resulting 5-cube compound on the right.


Truncated Cube and Dual Triakis Octahedron
As we have said, each of the 5 Platonic solids can be truncated to form one of the 13 Archimedean solids.
As we have seen with the tetrahedron, there are varying degrees of truncation that can occur.
Here we see a cube with tiny tetrahedra removed from the corners (1/4 Truncation):

Then, of course, we have the Archimedean solid, the truncated cube (Uniform truncation):

This creates the truncated cube, an Archimedean solid.
And lastly we have the deepest truncation of the cube (rectification) which produces the cuboctahedron, (vector equilibrium, Dymaxion), seen below. We will devote an entire article to this shape after we cover the octahedron. Remember that the octahedron and cube are duals. Together they create the cuboctahedron:

The Truncated Cube – 7920º
It has:
- 14 regular faces (6 octagonal and 8 triangular)
- 36 edges
- 24 vertices
The sum of its angles = 7920º
The Projections of the Truncated Cube
The following are some of the commonly encountered views:

Volume and Area of the Truncated Cube
Area = 2 (6 + 6√2 + √3) s2 s = side length
Volume = (21 + 14√2 s3)/3 s = side length
The Spherical Truncated Cube

Stereographic Projections of the Truncated Cube
Below we see the stereographic projections of the truncated cube with the octagon-centered on the left and the triangle-centered on the right.


The Net of the Truncated Cube

Its dual is the Triakis Octahedron, a Catalan solid.
If the truncated cube has edge length of 1, the triakis octahedron will have edge lengths of 2 and 2 + √2.
The Triakis Octahedron – 4320º
This Catalan solid, dual of the truncated cube, can be seen as an octahedron with triangular pyramids added to each face. There are three triangular faces for every face of an octahedron.

It has:
- 24 isosceles triangle Faces
- 36 Edges
- 14 Vertices
The faces look as follows:

The sum of its angles = 4320º.
The Projections of the Triakis Octahedron
Below are the orthogonal projections of the triakis octahedron with projective symmetry of 2 on the left, 4 in the center and 6 on the right.

The Triakis Octahedron Net

Snub Cube and Dual Pentagonal Icositetrahedron
We will now discuss the Archimedean solid, the Snub Cube and its Dual Catalan solid, the Pentagonal Icositetrahedron.
The Snub Cube – 7920º
The snub cube is an Archimedean solid.

It has:
- 38 Faces (6 squares and 32 equilateral triangles)
- 60 Edges
- 24 Vertices
The sum of its angles = 7920º. This is the same as the truncated tetrahedron.
It is chiral. That means it has two distinct forms that are mirror images (enantiomorphs) of each other. One is clockwise, the other counter-clockwise.
Of the 32 triangular faces, 8 of the triangles correspond with the vertices of a cube.
The other 24 triangles come in pairs and correspond to the 12 edges of the cube.
The Net of the Snub Cube:

Projections of the Snub Cube:

The Spherical Snub Cube:
The Stereographic Projection of the Snub Cube:

The snub cube can be generated by taking the six faces of the cube, pulling them outward so they no longer touch, then giving them each a small rotation on their centers until the spaces can be filled with equilateral triangles.
The snub cube can also be constructed from a transformed rhombicuboctahedron (Archimedean solid) by rotating the 6 blue square faces until the 12 white squares become pairs of equilateral triangles, seen below.

The Pentagonal Icositetrahedron – 12960º
The dual of the snub cube is the Catalan solid, the Pentagonal Icositetrahedron.

Like the snub cube, it also has two distinct forms which are mirror images (enantiomorphs). One spins counter-clockwise, as seen above. The other spins clockwise.
It has:
- 24 irregular pentagon Faces
- 60 Edges
- 38 Vertices
The Sum of its angles = 12960º. Note this number is exactly half a Precessional cycle of 25,920 years.
The faces look as follows:

The Pentagonal Icositetrahedron Net:

The Spherical Pentagonal Icositetrahedron:
- https://en.wikipedia.org/wiki/Cube
- MacKenzie, Kenneth, The Royal Masonic Encyclopedia, 1877
- Onstott, Scott, September 2014 AOM: Measuring the Mystery, 27 August 2014, https://grahamhancock.com/onstotts1/



Recent Comments