In this article we will complete our series of articles on the Dyad by delving even deeper into the symbolic and geometric aspects of the square roots of 2, 3, and 5.

Root Relationships
We explored the analogy of the geometric root to the stabilizing function of the plant root in Article 24.
The root cells of a plant are a powerful metaphor for the principle of integration and transformation.
Robert Lawlor tells us, “Transformation is the ubiquitous condition of the world, and their evolution from mineral to plant to animal, kingdom emerging out of kingdom, volume forming itself out of the converging vector extension of a preceding volume. There is periodicity, rhythm, oscillation, pattern, frequency, all measurable in time and space units.
This transformative moment is all that really exists; the phenomenal worlds are a transitory reflection.”

Plant roots are embedded in the earth.

Mathematical roots are embedded in the square.
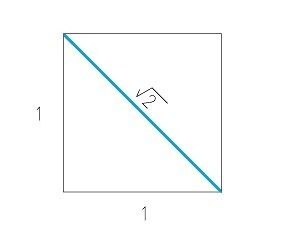
The plant depends upon the root for stability and nutrition.
The geometric root is an archetypal expression of this assimilative, generating, transformative function of the root.
The root of 2 contains the power of nature – it destroys in order to progress (it severs the initial square) and contains the power to instantaneously transform 1 into 2.
This mirrors the principle of the Octave in which halving = doubling. Growth occurs through a division within. One becomes Two.
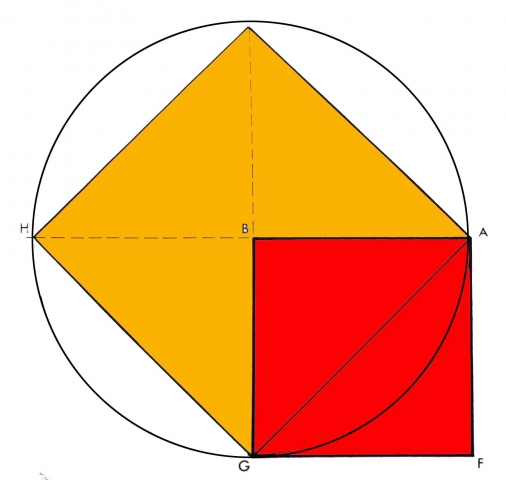
Lawlor explains, “The plant grows progressively out of a previous breaking down, but there is no rational theory which can explain how a flower or a squash can spring forth from a tender, narrow stem, like the explosion of one square out of another.”

The root is also the “generator of the change in the continuum of the ever-moving, irreversible phases which are a part of organic life.”1
The Root and the Germ
The seed immediately divides into root and germ.
This is an alternation of function.
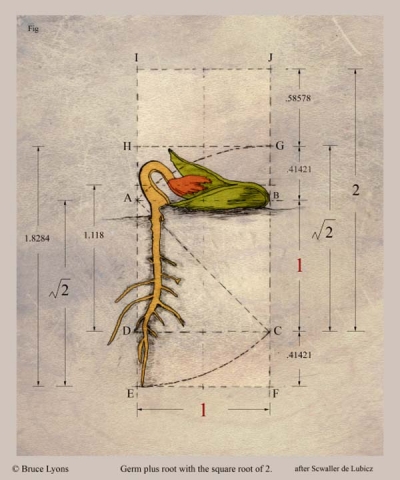
Credit: Bruce Lyons
R.A. Schwaller de Lubicz explains that the root principle represents a power botanists call ‘positive geotropism’.
This is the power to descend, involve and transmute from below.

The germ represents the power of ‘negative geotropism’.
This is the power to cause growth upwards and outwards.

It provides nourishment until the root begins to function, then it transforms into the first leaves.

This process involves the entire ascent culminating in the new seed.
“These are then polarized, directional opposites of the same power.”2
Reference Construction Lesson #17: The Square Root of 2, the Root and Germ & Principles of Alternation.
Principles of Alternation
The theoretical numerical progression of side to diagonal ratios is placed next to the geometric development to show graphically how quickly the whole number sequence approaches the irrational √2 function.
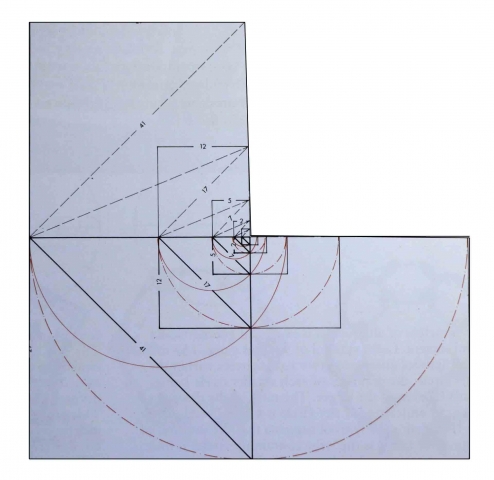
Credit: Robert Lawlor, Sacred Geometry: Philosophy & Practice
The root of square 1 becomes the germ of 2; the root of square 2 becomes the germ of 5; the root of square 5 becomes the germ of 12.
This illustrates a three-term proportion. a:b::b:c
That is, the geometric root/germ is to the universal root/germ as the universal root/germ is to the botanical expression of root and germ.

This reveals a precise demonstration, through the root of 2, of the Principle of Alternation:
- alternation in power (energetic, casual pulsation of the supra-rational root)
- alternation in the formal oscillation of squares produced by this power
- each coefficient oscillates above then below – coming closer to each time to the perfect ‘irrational’ state
Robert Lawlor tells us, “We are geometrically exploring an analogical, proportional thought, rather than following the more rigid, equational logic.”
We will now take a look at square root rectangles.
Square Root Rectangles
Square root rectangles are rectangles with a short side equal to 1 and a long side equal to the particular square root.
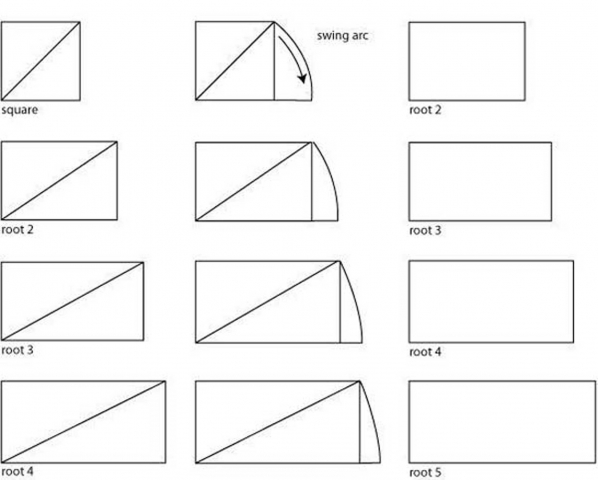
That is, a root-two rectangle has a short side of 1 and a long side of √2.
A root-three rectangle has a short side of 1 and a long side of √3.
A root-five rectangle has a short side of 1 and a long side of √5.
There are fascinating properties of the root rectangles as to how they fit together.
A square side 1 has a diagonal length of √2.
A √2 rectangle has a diagonal length of √3.
A √3 rectangle has a diagonal length of √4.
A √4 rectangle has a diagonal of length √5.
A √5 rectangle has a diagonal of length √6…etc
The root rectangles grow out of one another.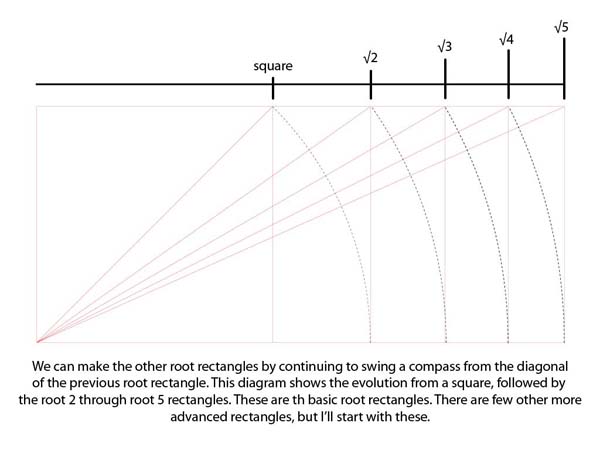
Square root rectangles have “eyes” situated at the point where a diagonal between two corners is cut by a perpendicular from one of the other corners. Below is a square root 2 rectangle divided into four, with the eye mapped out in the upper right rectangle.
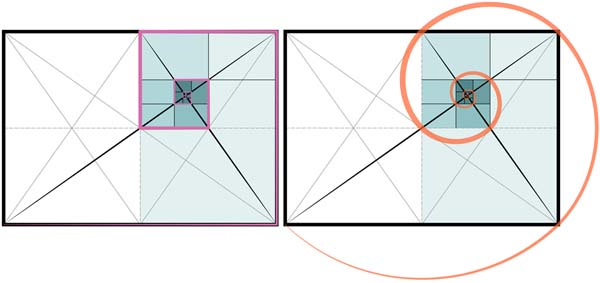
This is the eye of the fish in the Vesica.
“Uniquely, in the case of the root-three rectangle, the construction of its eye divides the rectangle into three equal parts.”3
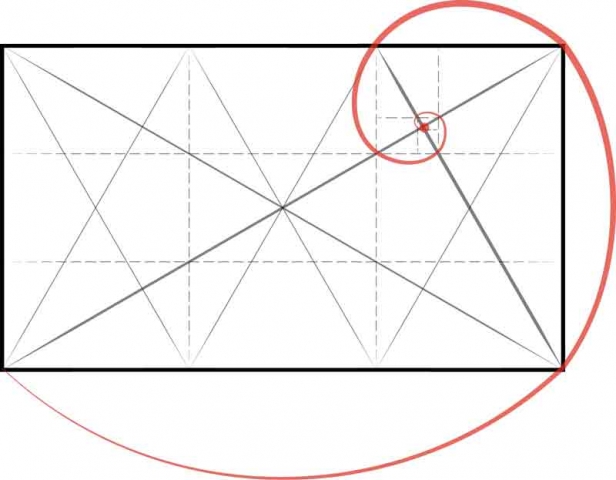
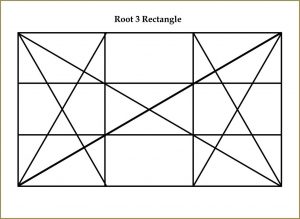
Reference Construction Lessons #18-21.
These include:
- 18. Root 2 Rectangles & Root 2 Spirals
- 19. Root 3 Rectangles & Root 3 Spirals
- 20. Root Rectangles & Phi
- 21. Expanding Root Ratios: Sacred Metrology
- Lawlor, Robert, Sacred Geometry: Philosophy & Practice, Thames & Hudson, 1982
- ibid.
- Michell, John, The Dimensions of Paradise,
Recent Comments